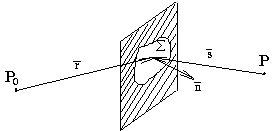
Пусть на пути сферической монохроматической световой волны, идущей от источника P0, располагается плоский непрозрачный объект с отверстием S, размеры которого велики по сравнению с длиной волны (рис.1). В соответствии с

|
| Рис.1. |
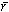 от
источника P0
до соответствующих участков объекта на поверхности
S
и от расстояния
от
источника P0
до соответствующих участков объекта на поверхности
S
и от расстояния 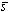 от этих участков
до точки P. В общем случае распределение поля U(P) может
быть найдено с помощью
интегральной формулы Френеля-Кирхгофа [1]
от этих участков
до точки P. В общем случае распределение поля U(P) может
быть найдено с помощью
интегральной формулы Френеля-Кирхгофа [1]
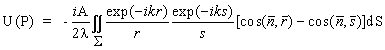
|
(1) |
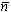 - вектор нормали к поверхности объекта;
- вектор нормали к поверхности объекта;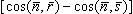 описывает изменение амплитуды вторичных
волн в зависимости от направления распространения падающей и вторичных волн.
Наиболее интересным для рассмотрения является случай, когда характерный линейный размер
отверстия b мал по сравнению с расстояниями
описывает изменение амплитуды вторичных
волн в зависимости от направления распространения падающей и вторичных волн.
Наиболее интересным для рассмотрения является случай, когда характерный линейный размер
отверстия b мал по сравнению с расстояниями 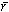 и
и 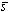 от точек P0 и P до объекта.
При этом как множитель
от точек P0 и P до объекта.
При этом как множитель 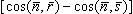 ,
так и член 1/rs изменяются при
интегрировании по отверстию S незначительно, и основную роль в
вычислении дифракционной
картины по формуле (1) играет интеграл от быстро
осциллирующего члена exp[-ik(r+s)].
Разложение в ряд этого члена (см. например [1, стр. 417])
позволяет существенно упростить
формулу (1).
,
так и член 1/rs изменяются при
интегрировании по отверстию S незначительно, и основную роль в
вычислении дифракционной
картины по формуле (1) играет интеграл от быстро
осциллирующего члена exp[-ik(r+s)].
Разложение в ряд этого члена (см. например [1, стр. 417])
позволяет существенно упростить
формулу (1).
Явления, описываемые в рамках такого приближения, носят название дифракции Френеля, или дифракции в ближней зоне. При r стремящемуся к бесконечности фронт падающей волны можно считать плоским. Если s стремится к бесконечности, то и вторичные волны, распространяющиеся под некоторым углом j к первоначальному направлению, образуют плоский волновой фронт. Дифракционные явления, наблюдаемые при этих условиях, носят название дифракции Фраунгофера, или дифракции в дальней зоне.
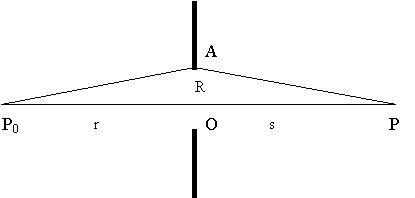
Различие между дифракцией Френеля и дифракцией Фраунгофера становится более наглядным, если ввести понятие зон Френеля. Для этого рассмотрим дифракцию на круглом отверстии радиуса R (рис. 2).
|
| Рис.2. |
Пусть источник света P0 и точка наблюдения P находятся на оси отверстия на расстояниях r и s соответственно. Выделим в плоскости объекта два вторичных источника: первый, расположенный на оси в точке О, и второй, расположенный на краю отверстия в точке А. Нетрудно показать, что свет, идущий из т. P0 в т. P через вторичный источник О, пройдет путь, равный r+s, а свет, прошедший через вторичный источник А - путь
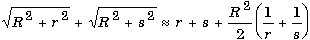 . .
|
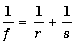
|
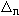 .
Говорят, что радиус отверстия R равен радиусу n-й зоны Френеля
Rn, если разность хода
.
Говорят, что радиус отверстия R равен радиусу n-й зоны Френеля
Rn, если разность хода
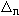 ,
соответствуюшая этому радиусу, составляет n длин полуволн, т.е.
,
соответствуюшая этому радиусу, составляет n длин полуволн, т.е.
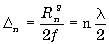
|
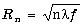 . .
|
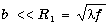 , ,
|
Настоящая задача физического практикума посвящена экспериментальному изучению явления дифракции, описываемой в рамках приближения Фраунгофера.

