![]()
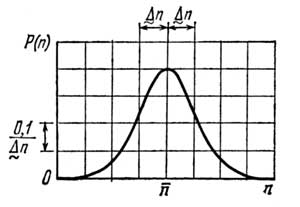
При больших N (N>>1) биномиальное распределение P(n) имеет острый максимум вблизи n . Для n не слишком удаленных от n, (N>>1, n = Np>>1 ) можно использовать распределения Гаусса (нормальное распределение):
![]()
где σ- стандартное отклонение.
 |
|
Гауссово распределение плотности вероятности P(n) как функция n. Вероятность того, что n принимает значения, лежащие между n-Δn и n+Δn определяется площадью под кривой, ограниченной этим интервалом. Если Δn равно стандартному отклонению, то эта площадь равна 0.683. |