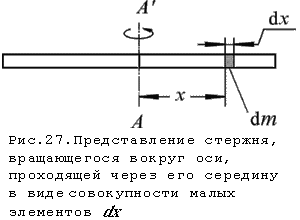
Пусть тонкий стержень имеет
длину
l и массу m.
Разделим
его на малые элементы длины
dx (рис.27), масса которых
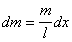. Если выбранный элемент находится
на расстоянии x от оси, то его момент
инерции
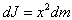, т.е.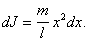 
Интегрируя последнее соотношение
в пределах от 0
до l/2 и удваивая
полученное выражение (для
учета левой половины стержня),
получим
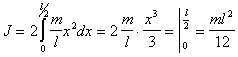(п.1)
Это выражение может быть получено
и другим способом, с помощью метода
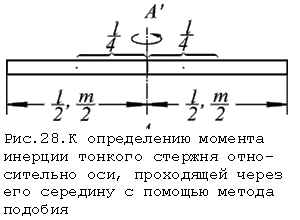
подобия. Будем считать, что рассматриваемый
стержень состоит из двух половин (рис.28).
Каждая из них имеет массу m/2
и длину l/2 .
Выражение для момента инерции стержня должно включать его массу и длину, так как это единственные параметры, определяющие его инерционные свойства при вращении. Пусть
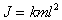(п.2)
где k- неизвестный коэффициент.
Для каждой из половин стержня
при вращении вокруг оси
AA` можно
найти момент инерции, используя
(п.2) и теорему Гюйгенса-Штейнера.
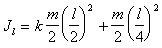(п.3)Полный момент инерции стержня
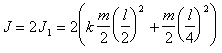(п.4)Но этот же момент инерции, согласно (п.2) равен kml2. Приравнивая (п.4) и (п.2) имеем
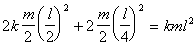(п.5)
или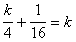 
и, следовательно,
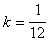(п.6)
т.е.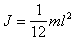 
, что совпадает с (п.1)
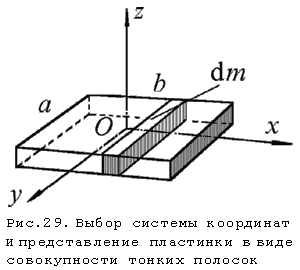Для расчета моментов
инерции прямоугольной
пластинки со сторонами
a и b и массой m
выберем систему координат так, чтобы ее
оси совпадали с главными центральными
осями (рис.29). Для прямоугольной пластинки
легко вычислить моменты инерции относительно
осей x и y.
Рассмотрим, например, расчет Jx.
Пластинку можно представить как совокупность тонких
полосок, для каждой из которых момент инерции
вычисляется так же, как для тонкой палочки длины
a . Момент
инерции пластинки относительно оси x
равен сумме моментов инерции этих полосок, т.е.
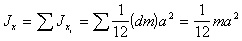(п.7)Аналогично вычисляется момент инерции пластинки относительно оси y
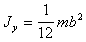(п.8)
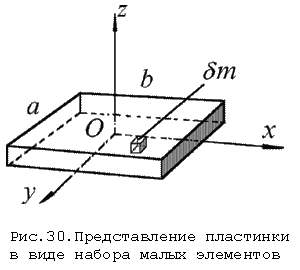Для вычисления момента инерции
пластинки относительно оси
z воспользуемся следующим
приемом. Рассмотрим малый элемент массы
$\delta\$ m
(рис.30). Его момент инерции
$\delta\$ Jz
относительно оси z равен
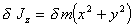(п.9)т.е. можно записать, что
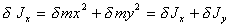(п.10)
где $\delta\$ Jy, $\delta\$ Jx
- моменты инерции этого малого элемента относительно осей
y и x.
Это же соотношение справедливо
не только для отдельного элемента,
но и для любого плоского тела в целом.
В этом легко убедиться, представляя плоское
тело как совокупность отдельных малых
элементов (рис.30) и производя суммирование
по всем этим элементам.
Таким образом, используя (п.7), (п.8) и (п.10), получим
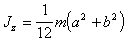(п.11)
Определим момент инерции треугольной пластины с помощью метода подобия. Этот метод используется обычно в тех случаях, когда изначально ясен общий вид формулы, определяющей момент инерции. В частности, если тело является правильной фигурой, например, квадратом, равносторонним треугольником, то в конечное выражение для момента инерции относительно оси, проходящей через центр масс и перпендикулярной плоскости фигуры, войдет масса тела и квадрат его характерного размера. Действительно - это единственные параметры, которые могут характеризовать инерционные свойства тела при его вращении вокруг выбранной оси. То есть можно записать
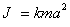(п.12)
где J
- момент инерции тела,
m - его масса,
a - характерный размер
(сторона квадрата или треугольника),
k - неизвестный коэффициент,
который определяется формой тела.
Для пластины в виде правильного
треугольника A`B`C`
(рис.31) момент инерции относительно оси,
перпендикулярной плоскости пластины и
проходящей через точку O,
может быть записан в виде (п.12).
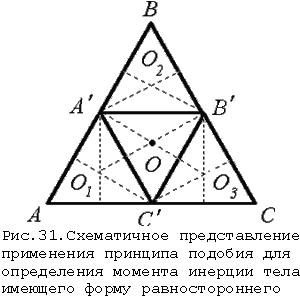Проведем геометрическое построение
(рис.31) и рассмотрим треугольную
пластину ABC со стороной 2a.
Очевидно, что ее масса будет равна 4m,
а формула для момента инерции будет иметь вид
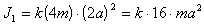(п.13)Пластина ABC состоит из четырех одинаковых треугольников со стороной a каждая. В этом случае момент инерции треугольника ABC можно представить в виде суммы моментов инерции четырех треугольных пластин. Для вычисления этих моментов инерции воспользуемся тем, что центр масс треугольника находится в точке пересечения его медиан. Обозначим через d расстояние от центров $\Delta\$ AA`C`, $\Delta\$ A`BB`, $\Delta\$ B`CC`, до точки O - центра масс пластины ABC. Используя теорему Гюйгенса-Штейнера, получаем
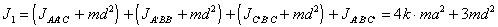(п.14)
Учитывая, что
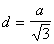и сравнивая (п.14) с (п.13), находим,что
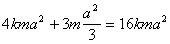(п.15)откуда следует
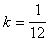(п.16)
То есть момент инерции плоского
тела, имеющего форму равностороннего
треугольника относительно оси, проходящей
через центр масс (точку О),
перпендикулярно его плоскости равен
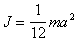(п.17)
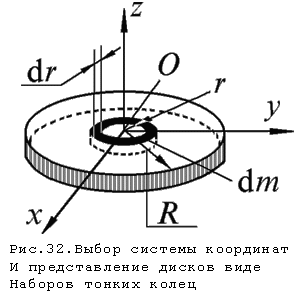Для расчета моментов инерции
тонкого диска массы m
и радиуса R
выберем систему координат так,
чтобы ее оси совпадали с главными
центральными осями (рис.32). Определим
момент инерции тонкого однородного диска
относительно оси z ,
перпендикулярной к плоскости диска.
Рассмотрим бесконечно тонкое кольцо
с внутренним радиусом r
и наружным r+dr.
Площадь такого кольца ds=2r $\pi$ dr,
а его масса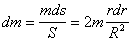 
,
где S= $\pi$ R2
- площадь всего диска. Момент инерции
тонкого кольца найдется по формуле
dJ=dmr2.
Момент инерции всего диска определяется интегралом
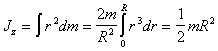(п.18)
Для определения Jx
воспользуемся симметрией диска
(Jx=Jy)
и утверждением (п.10), полученным при расчете
момента инерции прямоугольной пластины.
При этом из (п.10) получаем
Откуда
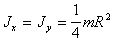(п.20)
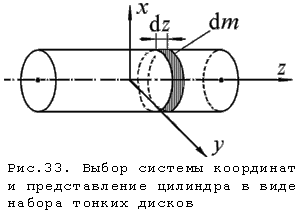Выберем оси системы координат,
совпадающие с главными центральными
осями так, как показано на рис.33.
Определим момент инерции цилиндра
относительно оси z.
Цилиндр представляет собой набор
тонких дисков с массами dm
и моментами инерции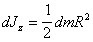 
.
Момент инерции цилиндра равен сумме моментов инерций
dJz
тонких дисков
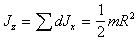(п.21)
где - радиус цилиндра, - его масса.
Пусть теперь ось вращения проходит
через центр масс цилиндра
перпендикулярно его продольной
оси (рис.33) и совпадает с осью
координат x.
Представим цилиндр как совокупность
тонких дисков толщиной dz,
массой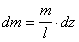 
( l - длина цилиндра).
Момент инерции тонкого диска
относительно оси Ox dJ`x
в соответствии с (п.20) и теоремой Гюйгенса-Штейнера равен
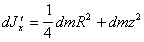(п.22)
где z - расстояние от диска до центра цилиндра.
Момент инерции всего цилиндра найдем после интегрирования по
z (по всей длине цилиндра)
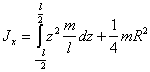(п.23)Откуда получаем
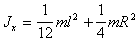(п.24)
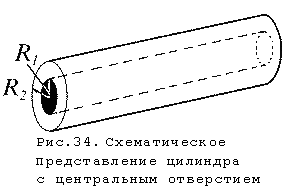
Однородный цилиндр массы
m с внешним радиусом
R2 и
внутренним радиусом
R1 (рис.34)
можно рассматривать как сплошной
цилиндр радиуса R2 ,
массы m2
, из которого вырезано отверстие - цилиндр радиуса
R1, массы
m1.
Очевидно, что
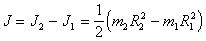и,т.к.
m=m2-m1
, и
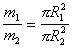, то
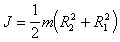(п.25)
Сплошной шар массы m
и радиуса R
можно рассматривать как совокупность
бесконечно тонких сферических слоев
с массами dm , радиусом r,
толщиной dr (рис.35).
Рассмотрим малый элемент сферического слоя $\delta$ m с координатами x, y, z. Его моменты инерции относительно осей проходящих через центр слоя - $\delta$ Jx, $\delta$ Jy, $\delta$ Jz, равны
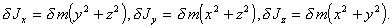
Т. е. можно записать
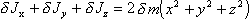(п.26)
Так как для элементов сферического
слоя x2+y2+z2=r2 то
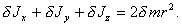
После интегрирования по всему объему слоя получим
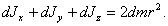(п.27)
Так как, в силу симметрии для сферического слоя
dJx=dJy=dJz=dJ
, а
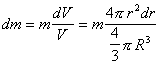, то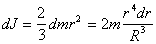 
Интегрируя по всему объему шара, получаем
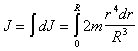
Окончательно (после интегрирования)
получим, что момент инерции шара относительно
оси, проходящей через его центр равен
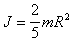(п.28)
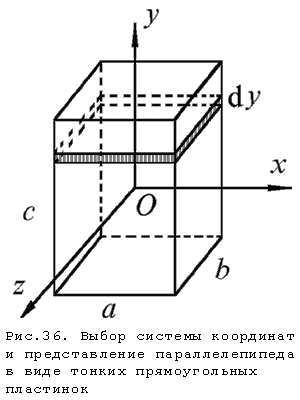Выберем оси системы координат
(x, y, z ) совпадающими
с главными центральными осями.
Начало системы координат совпадает
с центром параллелепипеда. Для
определения момента инерции
относительно оси Ox
представим параллелепипед как
совокупность тонких прямоугольных
пластинок (рис.36) массой
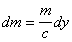и толщиной dy.
Момент инерции dJ`x
каждой такой пластинки относительно оси
Ox
в соответствии с (п.7)
и теоремой Гюйгенса-Штейнера равен
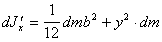(п.29)Момент инерции всего параллелепипеда получим, интегрируя по всему объему
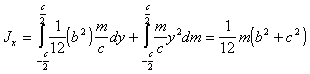(п.30)Аналогично вычисляются моменты инерции относительно осей y и x:
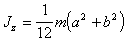(п.31)
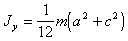(п.32)
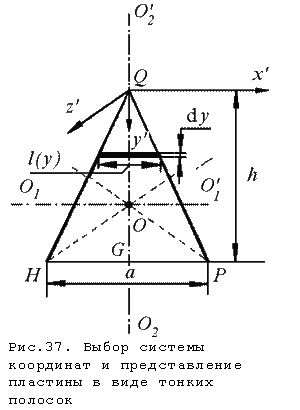Рассмотрим предварительно
моменты инерции тонкой равнобедренной
треугольной пластины HPQ (рис.37)
массы m1
относительно ее главных осей.
Центр пластины лежит на пересечении
медиан, причем
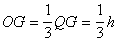(h - высота треугольника).
Главные центральные оси
O1O`1
и
O2O`2
такой пластины
расположены так, как показано на рис.37
(ось
O3O`3
проходит через точку O
перпендикулярно плоскости пластины).
Для удобства интегрирования введем
систему координат
x` , y` , x `
с началом в точке Q ,
так что Qz`
перпендикулярна плоскости
пластины, а оси
Qx` и
Qy`
лежат в плоскости
пластины и ось Qx`
перпендикулярна высоте
треугольника. Представим пластину как
набор тонких полосок толщиной
dy , с
массами dy и длинами l(y) , причем
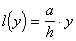(a - основание треугольника)
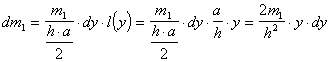(п.33)Момент инерции dJy каждой такой полоски относительно оси O2O`2 (совпадающей с осью y` ) равен (см.п.1)
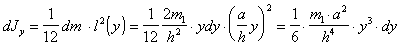(п.34)Полный момент инерции пластины J2 относительно оси O2O`2 получаем после интегрирования
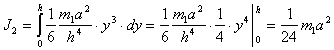(п.35)Момент инерции dJ`x каждой полоски относительно оси x` равен
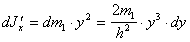(п.36)Для всей пластины
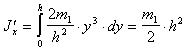(п.37)Момент инерции J1 относительно главной оси O1O`1 связан с J`x с помощью соотношения (теорема Гюйгенса-Штейнера)
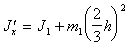(п.38)откуда получаем
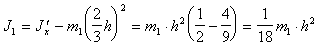(п.39)Для определения момента инерции пластины относительно оси O3O`3 ,перпендикулярной плоскости пластины, воспользуемся соотношением (п.10), верным для плоских тел
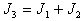(п.40)т.е.
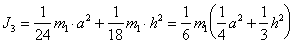(п.41)
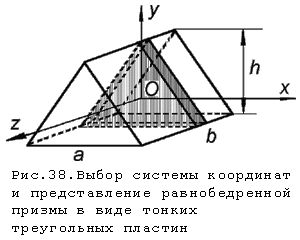Очевидно, что для пластины
в форме плоского равностороннего
треугольника, когда
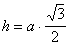выражение
(п.41) совпадает с (п.17),
полученным
более простым способом.
При определении
моментов инерции равнобедренной
призмы толщиной b и массой
m
представим ее как набор тонких
треугольных пластин с массами
.
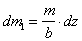Систему координат выберем так,
чтобы оси
x, y, z
совпадали с главными
центральными осями призмы (см.рис.38).
Момент инерции призмы относительно оси
Oz равен сумме моментов инерции отдельных
пластин
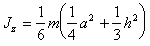(п.42)Получим теперь выражение для Jx и Jy . Момент инерции отдельной пластины J`1 относительно оси Ox в соответствии с (п.39) и теоремой Гюйгенса-Штейнера равен
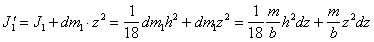(п.43)Интегрируя по всей высоте призмы, получаем момент инерции Jx относительно Ox
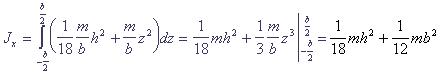(п.44)Для оси Oy имеем
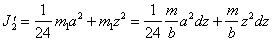(п.45)oткуда
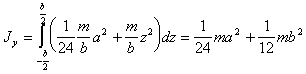(п.46)
Определим предварительно
моменты инерции для тонкой
полукруглой пластины, имеющей
массу m1 (рис.39).
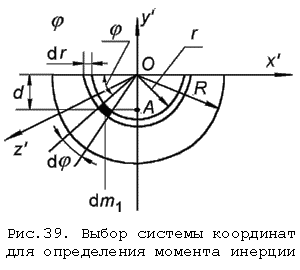
Найдем положение центра масс (т. А) этого тела, то есть расстояние d. По определению центра масс имеем
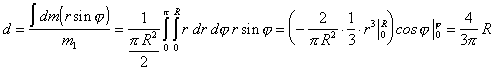(п.47)Выберем декартову систему координат x`, y`, z`, с центром в точке O (рис.39). Проводя прямое интегрирование так же, как для диска и учитывая, что J`x= J`y получаем
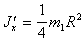(п.48)
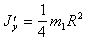(п.49)
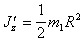(п.50)Моменты инерции, относительно главных центральных осей получаем, используя теорему Гюйгенса-Штейнера.
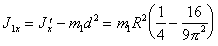(п.51)
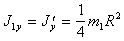(п.52)
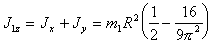(п.53)
При рассмотрении моментов
инерции полудиска массы m,
радиуса R и толщины
b представим его в
виде набора тонких пластин
так, как показано на рис.40.
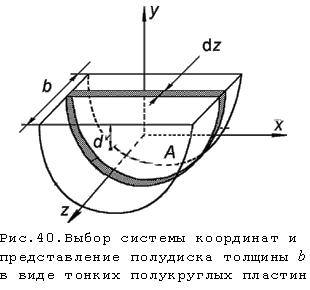
Систему координат выберем так, чтобы ее центр совпадал с центром масс полудиска, а направление осей координат - с направлением соответствующих главных центральных осей.
Моменты инерции dJx, dJy ,dJz тонких пластин с массами
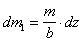, относительно осей
Ox, Oy и Oz
получаем на основании (п.51)-(п.53)
и теоремы Гюйгенса-Штейнера:
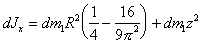(п.54)
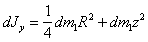(п.55)
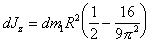(п.56)
где z - расстояние пластины от центра масс полудиска.
Выражения для моментов инерции
полудиска получаем после
интегрирования по всему объему
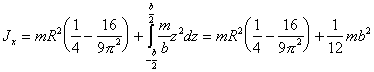(п.57)
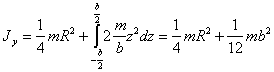(п.58)
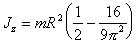(п.59)
| Форма тела | Моменты инерции |
Тонкий однородный стержень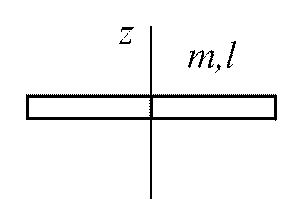 
|
 |
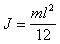Тонкая прямоугольная пластина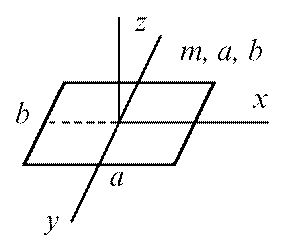
|
  
|
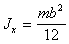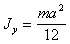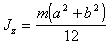
Параллелепипед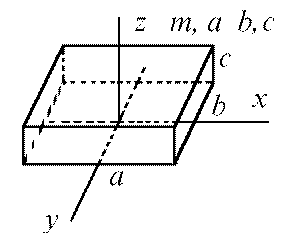
|
  
|
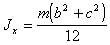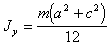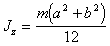
Тонкий диск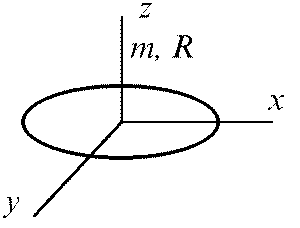
|
  
|
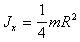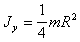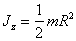
Цилиндр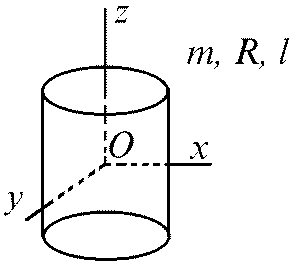
|
  
|
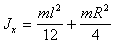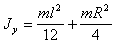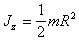
Плоский треугольник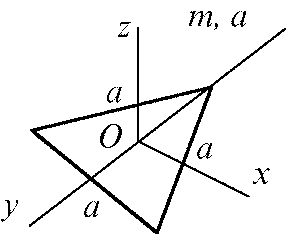
|
  
|
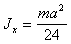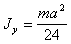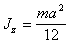
Треугольная призма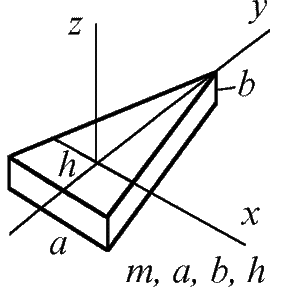
|
  
|
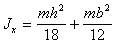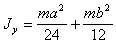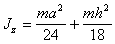
Полудиск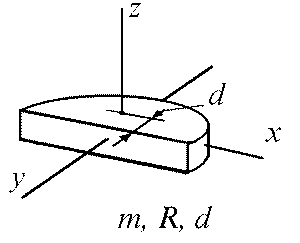
|
  
|
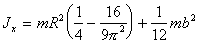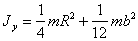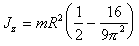
Шар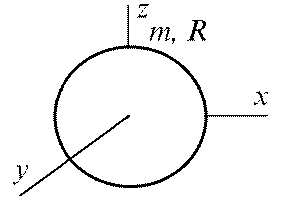
|
|
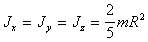
1. Сивухин Д.В. Общий курс физики. Т.1. Механика. 3-е изд. М.:Наука, 1989.§ 53.
2. Матвеев А.Н. Механика и теория относительности. 2-е изд. М.:Высшая школа, 1986.