Цель работы
С помощью крутильного
маятника,
представляющего
собой рамку с исследуемым
телом, закрепленную на упругом
подвесе, определяется момент
инерции тела относительно
закрепленной оси. Сравнивая
период колебания маятника без
тела и с телом, можно найти
момент инерции тела относительно
фиксированной оси. Компоненты
тензора инерции относительно
системы координат, жестко
связанной с телом, определяются
из нескольких таких опытов,
отличающихся направлением
оси вращения тела
при колебаниях маятника.
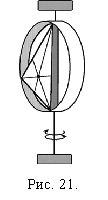
Рассмотрим колебания крутильного маятника, представляющего собой сложное тело, состоящее из рамки , закрепленной на вертикальной упругой проволоке, и исследуемого тела (рис.21). Действие момента сил упругости приводит к возникновению колебаний всей системы с периодом
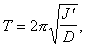 (6.1)
(6.1)Из соотношения (6.1) можно найти момент инерции J' :
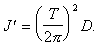 (6.2)
(6.2)Определяя период колебаний пустой рамки T0 , можно найти момент инерции маятника без тела - J0:
 (6.3)
(6.3)Для момента инерции исследуемого тела относительно фиксированной оси вращения получаем:
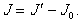 (6.4)
(6.4)Меняя положение тела относительно рамки, можно определять моменты инерции для осей вращения, имеющих различное направление относительно тела.
Тензор инерции будем рассматривать в системе координат, жестко связанной с телом. При этом, как показано во введении,
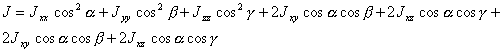 (6.5)
(6.5) ,
, 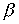 ,
, 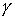 - углы, определяющие положение оси
вращения тела относительно системы
координат, связанной с исследуемым
телом.
- углы, определяющие положение оси
вращения тела относительно системы
координат, связанной с исследуемым
телом.
Используемая в задаче установка удобна для определения моментов инерции "плоских тел" - т.е. таких тел толщина которых значительно меньше их поперечных размеров. При этом одну из осей (например ось Oz), связанной с телом системы координат удобно направить перпендикулярно плоскости тела. Оси Ox и Oy находятся в плоскости тела и их направления произвольны, начало координат совпадает с центром масс тела и находится на оси вращения (рис.22). При этом один из направляющих косинусов ( cos
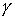 )
равен нулю, и вместо
(6.5) получим
)
равен нулю, и вместо
(6.5) получим
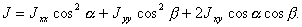 (6.6)
(6.6)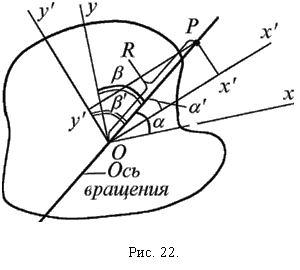 Величина J
- момент инерции
данного тела при
вращении вокруг определенной
оси , проходящей через его центр
масс. При повороте системы координат
(осей Ox и Oy
в своей плоскости), величина
момента инерции J
не изменяется, но каждой
ориентации осей соответствует
свои значения компонент тензора
инерции Jxx , Jyy
и Jxy=Jyx
Величина J
- момент инерции
данного тела при
вращении вокруг определенной
оси , проходящей через его центр
масс. При повороте системы координат
(осей Ox и Oy
в своей плоскости), величина
момента инерции J
не изменяется, но каждой
ориентации осей соответствует
свои значения компонент тензора
инерции Jxx , Jyy
и Jxy=Jyx
При определенном выборе системы координат, когда направления осей Ox' и Oy' совпадают с главными осями инерции тела, Jxy= Jyx= 0, и вместо (6.6) имеем
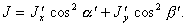 (6.6a)
(6.6a) '
и cos
'
и cos 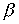 '
- направляющие косинусы
выбранной ранее оси вращения
в новых осях координат
Ox' ,
Oy' ,
Jx'
и Jx'
- компоненты тензора инерции
в системе координат, оси которой
совпадают по направлению с главными
осями инерции.
'
- направляющие косинусы
выбранной ранее оси вращения
в новых осях координат
Ox' ,
Oy' ,
Jx'
и Jx'
- компоненты тензора инерции
в системе координат, оси которой
совпадают по направлению с главными
осями инерции.
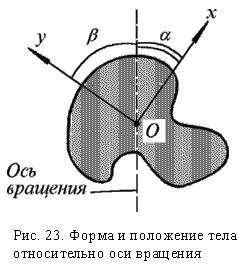
Выберем на оси вращения некоторую точку P, находящуюся на расстоянии R от начала координат и имеющую координаты x' и y'. Пусть величина R численно равна
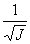 .
При этом
.
При этом
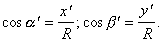 Подставив эти величины в (6.7а), получим, что
Подставив эти величины в (6.7а), получим, что
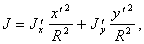
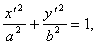 (6.6б)
(6.6б)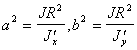 , a
и b являются постоянными величинами.
, a
и b являются постоянными величинами.
Уравнение (6.6б) является каноническим уравнением эллипса в координатах x' , y', полуоси которого
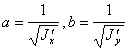 .
.
 Эллипс (6.6б) является сечением
эллипсоида инерции плоскостью
x' , y'.
Эллипсоидом инерции называется поверхность,
характеризующая величины моментов инерции
твердого тела относительно множества
возможных осей вращения, проходящих
через одну точку ( в данном случае
через центр масс тела). При этом
для каждого направления вдоль оси l
откладываются отрезки, численно равные величине
Эллипс (6.6б) является сечением
эллипсоида инерции плоскостью
x' , y'.
Эллипсоидом инерции называется поверхность,
характеризующая величины моментов инерции
твердого тела относительно множества
возможных осей вращения, проходящих
через одну точку ( в данном случае
через центр масс тела). При этом
для каждого направления вдоль оси l
откладываются отрезки, численно равные величине
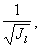 где Jl
- момент инерции тела
относительно оси l.
Концы этих отрезков образуют
поверхность, называемую
эллипсоидом инерции
(трехмерное уравнение эллипсоида
инерции может быть получено из (6.5)).
где Jl
- момент инерции тела
относительно оси l.
Концы этих отрезков образуют
поверхность, называемую
эллипсоидом инерции
(трехмерное уравнение эллипсоида
инерции может быть получено из (6.5)).
Пусть исследуемое тело имеет форму, показанную на рис.23. Точка O - центр масс тела. Оси Ox и Oy выбраны произвольно. Тело закреплено в рамке крутильного маятника так, что точка O лежит на оси вращения, а положение тела характеризуется углом
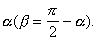
Если тело закреплено в рамке так, как показано на рис.24а, то
 = 0 и
= 0 и
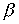 =
= 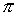 /2 Из (6.6) получаем, что
/2 Из (6.6) получаем, что
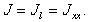 (6.7)
(6.7)При закреплении тела, соответствующем рис.24б,
 =
= 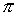 /2 и
/2 и 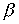 = 0.
И, следовательно, из (6.6) получаем, что
= 0.
И, следовательно, из (6.6) получаем, что
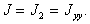 (6.8)
(6.8)При повороте тела в своей плоскости на угол
 0
(рис.24в) и -
0
(рис.24в) и -  0
(рис.24г) относительно оси вращения получаем, соответственно,
0
(рис.24г) относительно оси вращения получаем, соответственно,
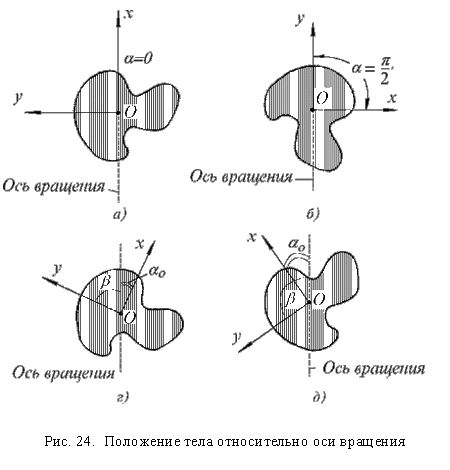
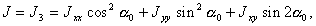 (6.9)
(6.9)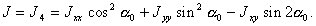 (6.10)
(6.10)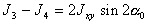 или
или 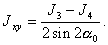 (6.11)
(6.11)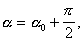 то
то
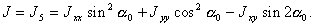 (6.12)
(6.12)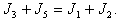 (6.13)
(6.13)Экспериментальное определение величин J1 , J2 , J3 и J4 дает возможность найти четыре отличных от нуля компоненты тензора инерции плоского тела: Jxx , Jyy , Jxy = Jyx для заданной системы координат. Если оси координат Ox и Oy совпадают с главными осями инерции тела, то Jxy = Jyx Соотношение (6.13) может служить проверкой правильности проведенного эксперимента.
Экспериментальная установка показана на рис.25 или AVI (6.6M) . Она состоит из стойки и рамки, закрепленной на упругом подвесе. Исследуемые тела поочередно крепятся в рамке с помощью винта.
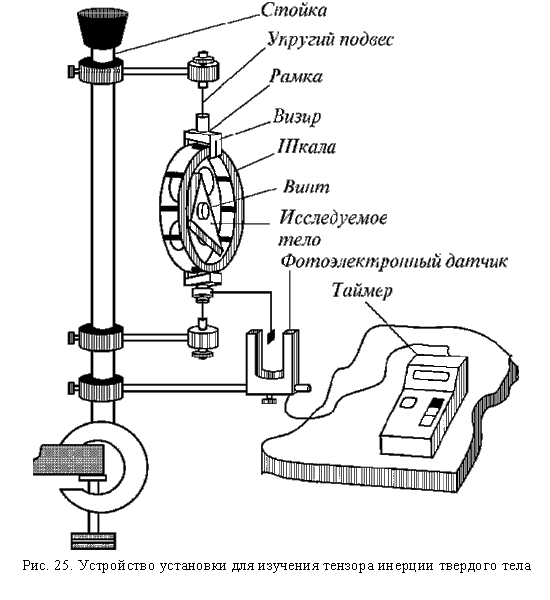
Установка снабжена системой автоматического отсчета времени и числа периодов, включающей в себя таймер и фотоэлектронный датчик.
Упражнение 1. Определение коэффициента упругости подвеса и момента инерции пустой рамки.
Определение упругости нити подвеса осуществляется из результатов изучения колебаний длинного металлического стержня, закрепленного с помощью специального приспособления в рамке перпендикулярно оси вращения. Предполагается, что предварительно измерена его длина и масса и вычислен его момент инерции, а также определены погрешности этих величин (результаты измерений и расчетов необходимо внести в табл.6.1)
Таблица 6.1
| Длина стержня L = | SL = |
| Масса стержня m = | Sm = |
| Момент инерции стержня относительно оси проходя- щей через центр масс перпендикулярной стержню, J = |
SJ = |
- Измерить время tn n=10-20 колебаний пустой рамки. Измерения провести несколько раз, данные занести в табл.6.2.
- Закрепить стержень в рамке симметрично. Измерить время tn 10-20 колебаний рамки со стержнем. Измерения провести несколько раз, данные занести в табл.6.2.
- Для каждого опыта определить периоды колебаний пустой рамки T0 и рамки со стержнем T2.
- Найти средние арифметические значения < T0 > и < T2 > и выборочные стандартные отклонения для этих величин ST0 , ST2 . Результаты вычислений внести в табл.6.2.
-
Учитывая, что период
колебаний крутильного
маятника связан с моментом
инерции соотношением (6.1),
получаем, что
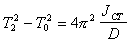 ,
где Jст - вычисленный ранее момент инерции стержня.
,
где Jст - вычисленный ранее момент инерции стержня.
Отсюда следует, что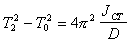 .
.
Используя последнее соотношение, определить коэффициент упругости подвеса, а затем по формуле (6.3) - момент инерции пустой рамки J0.
Таблица 6.2
| Колебания без стержня | Колебания со стержнем | ||||||||||
| N | tn | n | T0 | < T0 > | ST0 | N | tn | n | T2 | < T2 > | ST2 |
| 1 | 1 | ||||||||||
| 2 | 2 | ||||||||||
| 3 | 3 | ||||||||||
| .... | |||||||||||
- Для выполнения работы необходимо измерить размеры одного из тел по указанию преподавателя (ребра параллелепипеда, стороны треугольной призмы, радиус полудиска). Данные занести в табл.6.3.
- Все тела, исследуемые в данной задаче, закрепляются в рамке благодаря ее конструкции, таким образом, что центр масс лежит на оси вращения. Закрепив в рамке выбранное тело, измеряют время tn n=10-20 колебаний. Проводят несколько таких измерений. Поворачивают рамку на небольшой угол (например на 150), и вновь измеряют время tn. Снова поворачивают рамку на тот же угол и проводят измерения tn . Так поступают до полного поворота рамки на 1800. Результаты каждого измерения заносят в табл.6.3.
Таблица 6.3
| Форма и размеры исследуемого тела: | ||||||||
| N |  i i |
tn | n | T | < T  > > |
ST  |
J  |
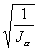 |
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| .... | ||||||||
-
Находят периоды
колебаний маятника
для каждого значения
 ,
их среднее значение < T
,
их среднее значение < T  >
и выборочные стандартные отклонения
ST
>
и выборочные стандартные отклонения
ST  .
Величины заносят в табл.6.3.
.
Величины заносят в табл.6.3.
-
Определяют моменты
инерции исследуемого
тела по формулам (6.2)
- (6.4) для различных
значений
 .
Данные заносят в табл.6.3.
.
Данные заносят в табл.6.3.
-
Строят в полярных
координатах R(
 ) ,
сечение эллипсоида инерции
) ,
сечение эллипсоида инерции
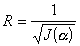 для исследованного тела,
считая ,что J(1800+
для исследованного тела,
считая ,что J(1800+  )=J(
)=J(  ) .
На этом же графике необходимо нарисовать и исследуемое
тело.
) .
На этом же графике необходимо нарисовать и исследуемое
тело.
- Определяют положения рамки, при которых момент инерции принимает максимальное и минимальное значения. Эти положения соответствуют главным центральным осям инерции изучаемого тела.
- Используя известные формулы (см. Приложение), рассчитывают величины моментов инерции тела относительно всех трех главных центральных осей и сравнивают полученные значения с экспериментальными. При этом теоретическое значение Jz сравнивается с суммой значений Jx , Jy , полученной экспериментально, поскольку для плоских тел (см. Приложение) Jz=Jx+Jy.
Для выполнения этого упражнения используется то же тело, что и в упр.2. На поверхности всех тел, входящих в комплект установки нанесены прямые, проходящие через точку, соответствующую его центру масс и повернутые относительно друг друга на 150. За ось Ox системы координат, связанной с телом, следует принять направление одной из этих прямых.
-
Определить четыре
величины момента инерции тела
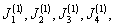 для случая, когда выбранная ось
Ox, соответственно ,
совпадает , перпендикулярна,
составляет угол
для случая, когда выбранная ось
Ox, соответственно ,
совпадает , перпендикулярна,
составляет угол
 0
и -
0
и -  0
с осью вращения (
0
с осью вращения (  0
- произвольный угол, например 300
или 450).
Для выполнения этого пункта
необходимо произвести измерения,
аналогичные проведенным в упр.2.
Результаты занести в табл.6.4.
0
- произвольный угол, например 300
или 450).
Для выполнения этого пункта
необходимо произвести измерения,
аналогичные проведенным в упр.2.
Результаты занести в табл.6.4.
-
Приняв за ось Ox
другое направление, повторить
все измерения п.1 и получить
новые значения величин
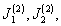
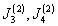 . Полученные результаты
занести в таблицу, аналогичную табл.6.4.
. Полученные результаты
занести в таблицу, аналогичную табл.6.4.
-
Воспользовавшись
измеренными величинами
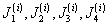 и соотношениями (6.7) - (6.10)
определить Jxx ,
Jyy ,
Jxy
для двух систем координат,
которые использовались в п.1
и п.2. Убедиться, что компоненты
тензора инерции зависят от выбора
системы координат и занести их в
табл. 6.4, указать ориентацию
системы координат, для которой
они получены.
и соотношениями (6.7) - (6.10)
определить Jxx ,
Jyy ,
Jxy
для двух систем координат,
которые использовались в п.1
и п.2. Убедиться, что компоненты
тензора инерции зависят от выбора
системы координат и занести их в
табл. 6.4, указать ориентацию
системы координат, для которой
они получены.
Таблица 6.4
| Форма и размеры исследуемого тела: | |||||||||
| N | tn | n | < T > | S< T > | J i | S J i | |||
| 1 | Ось Ох парал- лельна оси вра- щения |
1 | J xx = | ||||||
| 2 | |||||||||
| 3 | |||||||||
| 2 | Ось Ох пер- пендикулярна оси вращения |
1 | J уу = | ||||||
| 2 | |||||||||
| 3 | |||||||||
| 3 | Ось Ох со- ставляет угол  0 с осью 0 с осью вращения |
1 | J xy = | ||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | Ось Ох со- ставляет угол -  0 с осью 0 с осью вращения |
1 | |||||||
| 2 | |||||||||
| 3 | |||||||||
| .... | |||||||||
Изучаемое тело представляет собой крестовину из стержней заданной массы и длины и шаров. Шары закрепляются на крестовине с помощью винтов. В упражнении по указанию преподавателя исследуется одна из трех
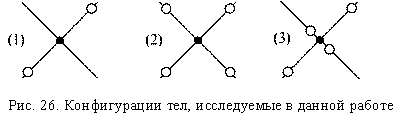
- Закрепить тело в рамке. Измерить периоды колебаний маятника для нескольких заданных положений рамки, изменяя угол, определяющий ее положение относительно оси вращения на 150, начиная от положения при котором два шара находятся на одной вертикали (аналогично п.2 упражнения 2). Результаты измерений занести в табл.6.5.
- Определить моменты инерции маятников относительно выбранной оси для всех рассмотренных случаев (аналогично п.2 упражнения 2).
- Определить компоненты тензора инерции выбранного тела Jxx , Jyy , Jxy для системы координат, связанной со стержнями крестовины.
-
Используя известные
формулы для моментов
инерции стержня и шара
(см. Приложение), определить
моменты инерции тела относительно
вертикальной оси для использованных
значений . Построить в полярной
системе координат сечения эллипсоидов
инерции
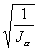 и
и
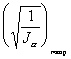 по найденным экспериментальным
и теоретическим данным .
по найденным экспериментальным
и теоретическим данным .
Таблица 6.5
| Выбранная конфигурация системы тел: | ||||||||
 i i |
N | tn | n | T  , < T , < T  > > |
ST  |
J  |
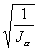 |
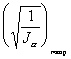 |
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| 1 | ||||||||
| 2 | ||||||||
| 3 | ||||||||
| .... | ||||||||
В результате выполнения работы должно быть экспериментально получено сечение эллипсоида инерции плоскостью исследованного тела. Определены направления главных центральных осей инерции и определены компоненты тензора инерции для двух ориентаций осей и . Следует провести сравнение данных эксперимента с теорией. Для тела в виде крестовины для одного расположения системы координат должны быть определены экспериментально и теоретически компоненты тензора инерции, построены экспериментально и теоретически определенные сечения эллипсоидов инерции.
Контрольные вопросы
Записать уравнения моментов и объяснить смысл входящих в него величин.
Какова связь между моментом импульса и угловой скоростью? Что такое тензор инерции?
Записать компоненты тензора инерции для простейших систем: тонкая палочка, система материальных точек.
Что такое главные оси? Что такое центральные оси? Примеры.
Как направлены векторы угловой скорости и момента количества движения тела вокруг закрепленной оси
1) если ось вращения совпадает с одной из главных осей;
2) если ось вращения не совпадает ни с одной из главных осей?Связь между компонентами тензора инерции и моментом инерции относительно фиксированной оси.
Что такое эллипсоид инерции? Как с помощью эллипсоида инерции определить значение момента инерции тела относительно заданной оси?
Сивухин Д.В. Общий курс физики. Т.1. Механика, 3-изд., М.: Наука, 1989.
Петкевич В.В. Теоретическая механика. М.: Наука, 1981, гл.VI, §1.
Ольховский И.И. Курс теоретической механики для физиков. М.: Из-во Моск.ун-та, 1974, § 38.