Цель работы
Идея эксперимента заключается
в исследовании вращательного
и колебательного движений твердого
тела правильной формы относительно
различных осей, проходящих через
центр масс и определения на основе
данных эксперимента главных
моментов инерции. В процессе работы
устанавливается связь между моментом
инерции относительно произвольной
фиксированной оси и компонентами
тензора инерции.
Рассмотрим твердое тело,
закрепленное
таким образом,
что оно может
вращаться вокруг некоторой
неподвижной точки O.
Тензор инерции
будем рассматривать в
системе координат, жестко
связанной с телом. Существует
связь между моментом импульса
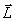 тела и угловой частотой
тела и угловой частотой
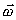 (см. введение)
(см. введение)
 , (5.1)
, (5.1)где
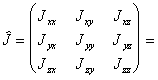
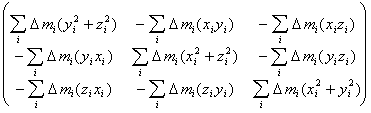 . (5.2)
. (5.2)В том случае, когда вращение твердого тела происходит относительно произвольной закрепленной оси AA', проходящей через точку O, проекция моменета импульса тела, относительно точки О на эту ось равна (см. рис. 16)
 , (5.3)
, (5.3)
где 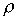 i - расстояние
от i-го элемента тела
до оси AA' , а величина
i - расстояние
от i-го элемента тела
до оси AA' , а величина
 (5.4)
(5.4)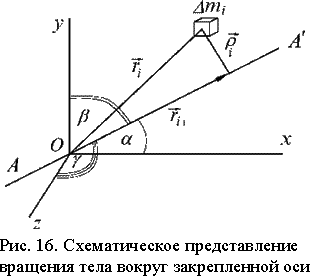
является моментом инеции относительно закрепленной оси.
Значение момента инерции J твердого тела относительно оси, имеющей произвольное направление, связано с компонентами тензора инерции соотношением (В.25).
В дальнейшем будем
использовать такую
систему координат,
оси которой совпадают
с главными осями инерции.
В этом случае тензор
инерции будет иметь
диагональный вид, а соотношение
(В.25) запишется так:
 . (5.5)
. (5.5)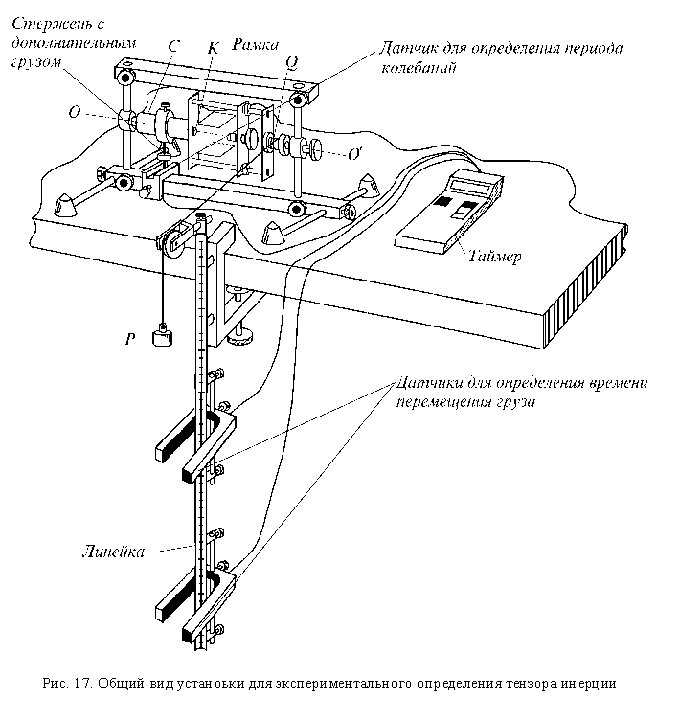
Экспериментальная установка смонтирована на основании, на котором установлены две стойки с направляющими для винтов, положение одного из которых может регулироваться. Экспериментальная установка показна на рис.17, а так же для упражнения 1 AVI (9.9M) и упражнения 2 AVI (4.1M). Эти винты вставляются в подшипники, которые закреплены в рамке специальной конструкции, в результате этого рамка может вращаться вокруг горизонтальной оси (на рис.17 это ось OO'). Рамка состоит из двух планок, (одна из которых на рис.17-левая) соединена с цилиндром С, другая - со шкивом Q. Эти планки зафиксированы на определенном расстоянии двумя направляющими. На планке с цилиндром установлен конус K для крепления исследуемого тела. По направляющим перемещается подвижная планка. Эта планка может фиксироваться на направляющих с помощью цанговых зажимов (для этого необходимо повернуть винты на них). В центре подвижной планки имеется винт с конусным наконечником. Исследуемое тело фиксируется между конусом неподвижной левой и конусным винтом подвижной планок, для чего в исследуемых телах имеются специальные углубления.
Закрепление исследуемых тел в рамке может осуществляться передвижением подвижной планки (при отжатых винтах цангового зажима) и вращением винта с коническим наконечником (этим вращением осуществляется более точная установка).
Рамка с исследуемым телом может совершать как вращательное, так и колебательное движение. Вращение происходит при опускании груза P, висящего на нити, намотанной на шкив Q. Масса груза и радиус шкива указываются на установке.
Установка снабжена системой автоматического отсчета времени, включающей в себя таймер и два фотоэлектронных датчика для определения времени перемещения груза. Расстояние между датчиками определяется по линейке, укрепленной на установке.
Для определения периодов колебаний рамки с исследуемым грузом на цилиндре C устанавливается кольцо со стержнем, на котором закреплен дополнительный груз, устанавливаемый в различных положениях. Установка снабжена системой автоматического отсчета периода, включающей в себя таймер и фотоэлектронный датчик для определения периода колебаний.
В работе определяются
компоненты тензора инерции
однородного металлического
параллелепипеда (рис.18)
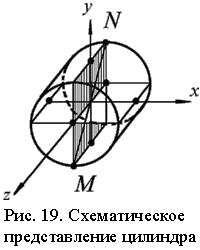
и цилиндра (рис.19).
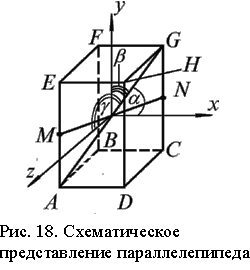
Упражнение 1. Изучение тензора инерции динамическим методом.
Рассмотрим приращение тела правильной формы, закрепленного в рамке, вокруг некоторой оси под действием момента внешних сил. Момент внешних сил создается с помощью нити, намотанной на шкив, к концу которой подвешен груз массы m (рис.20) В качестве исследуемого тела используется параллелепипед.
Пусть груз начал
движение от отметки
x0,
затем прошел отметку
x1
со скоростью
v1.
и, через время t.
после этого - отметку
x2.
со скоростью
v2.
На основании закона
сохранения механической
энергии можно записать:
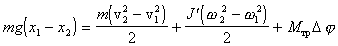 , (5.6)
, (5.6)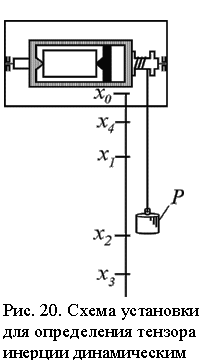
где mg=(x1-x2)
- изменение
потенциальной энергии груза,
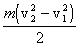 -изменение его кинетической энергии,
-изменение его кинетической энергии,
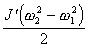 - изменение кинетической
энергии вращательного
движения рамки с телом,
Mmp
- изменение кинетической
энергии вращательного
движения рамки с телом,
Mmp 
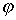 - работа сил трения в оси рамки,
m - масса груза,
подвешенного на нити,
J'=J+J0
- момент инерции
тела (J) и рамки (J0),
w1 , w2
- угловые скорости вращения рамки
для положений груза в точках
x=x1 и x=x2
соответственно,
g
- ускорение свободного падения,
Mmp
- момент сил трения,
- работа сил трения в оси рамки,
m - масса груза,
подвешенного на нити,
J'=J+J0
- момент инерции
тела (J) и рамки (J0),
w1 , w2
- угловые скорости вращения рамки
для положений груза в точках
x=x1 и x=x2
соответственно,
g
- ускорение свободного падения,
Mmp
- момент сил трения,
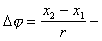 - угол, на который повернулась
рамка при прохождении
груза между отметками
x1 и x2 , r
- радиус шкива.
- угол, на который повернулась
рамка при прохождении
груза между отметками
x1 и x2 , r
- радиус шкива.
Учитывая,
что v=wr,
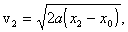 ,
,
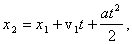 ,
где a
- ускорение груза,
t
- время
прохождения грузом
x1 - x2,
расстояния получаем:
,
где a
- ускорение груза,
t
- время
прохождения грузом
x1 - x2,
расстояния получаем:
 , (5.7)
, (5.7)
Для момента
инерции пустой
рамки (без тела) имеем:
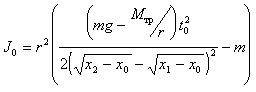 , (5.8)
, (5.8)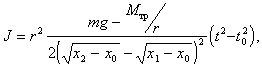 . (5.9)
. (5.9)Пользуясь этой формулой, можно определять моменты инерции тела относительно произвольных осей. Это можно сделать, в частности для главных центральных осей, совпадающих с выбранными осями координат (Jx , Jy , Jz, а также для осей, совпадающих с одной из диагоналей параллелепипеда, например AG (JAG) или MN (JMN) (см.рис.18), выразив их соответственно через времена опускания груза tx , ty , tz , tAG , tMN.
Момент сил трения,
входящий в (5.9), можно
оценить следующим
образом. Если опустить
груз на отметке
x0, то он после
опускания до нижней точки
x3
поднимется затем до отметки
x4.
Разность значений потенциальной
энергии груза в точках
x4
и
x0
и будет равна работе сил трения.
То есть
 , (5.10)
, (5.10)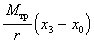 - работа сил трения
при движении груза
вниз от верхней
точки до полного
разматывания нити,
- работа сил трения
при движении груза
вниз от верхней
точки до полного
разматывания нити,
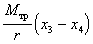 - работа сил
трения при подъеме груза.
Из (5.10) следует
- работа сил
трения при подъеме груза.
Из (5.10) следует
 . (5.11)
. (5.11)
Пусть размер параллелепипеда
(см. рис. 18)
по оси Ox равен
a,
по оси
Oy - b,
по оси Oz - c .
Квадраты направляющих
косинусов для его диагонали AG
соответственно равны
 (5.12)
(5.12)
Подстановка уравнений (5.9)
(для различных осей вращения)
и (5.12) в формулу
(5.5) для момента
инерции относительно
закрепленной оси дает
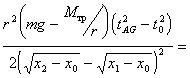
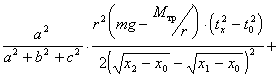
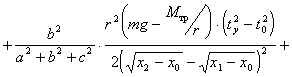
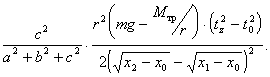
Так как сумма
квадратов направляющих
косинусов равна единице,
то получаем:
 (5.13)
(5.13)Эта закономерность можно проверить экспериментально.
Для выполнения работы необходимо измерить радиус шкива r и размеры тела (ребра параллелепипеда) a, b, c. Величины a, b, c, r измеряют штангенциркулем не менее трех раз в различных сечениях тела, заносят их в табл. 5.1.
Таблица 5.1
№ a <a> , S<a> b <b> , S<b> c <c> , S<c> r в<r> , S<r> 1 2 3 Заносят в таблицу 5.2 значения xo , x1 , x2 , x3 . Взвешивают груз P и заносят в табл. 5.2 его массу.
Определяют время опускания груза P при пустой рамке to . Для этого нить, имеющую на конце груз, аккуратно виток к витку наматывают полностью на шкив. Освобождают груз. Измерение времени необходимо проводить не менее трех раз. Данные заносят в таблицу 5.2. Одновременно для каждого опыта в таблицу заносят значения x4.
Таблица 5.2
Параметры
исследуемой
системыN t0 <t0> , St0 x4 <x4> 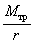
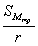
x0 =
x1 =
x2 =
x3 =
m =
1 2 3 4 5 Закрепляют в рамке параллелепипед в разных положениях и измеряют времена tx , ty , tz , tAG , tMN не менее трех раз. Результаты заносят в табл. 5.3.
Таблица 5.3
№ tx <tx> ,
S<tx>ty <ty> ,
S<ty>tz <tz> ,
S<tz>tAG <tAG> ,
S<tAG>tMN <tMN> ,
S<tMN>1 2 3
Определяют среднее арифметические значения a, b, c, r и выборочные стандартные отклонения для этих величин. Данные заносят в табл. 5.1.
Находят средние арифметические значения и выборочные стандартные отклонения для t0 и x4. Данные заносят в табл. 5.2. По формуле (5.11) находят величину
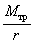 и погрешность ее определения.
и погрешность ее определения.
Находят средние арифметические значения tx , ty , tz , tAG , tMN и погрешности их определения. Результаты заносят в табл. 5.3.
По формуле (5.9) находят экспериментальные значения величин Jx , Jz , JMN и их погрешности. Данные заносят в табл. 5.4.
В связи с тем, что ось MN лежит в плоскости xz, поэтому соотношение (5.5) для JMN принимает вид
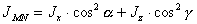 .
Подставляя
в это выражение
определенные
в п.4 значения
Jx , Jy
вычисляют теоретическое
значение
.
Подставляя
в это выражение
определенные
в п.4 значения
Jx , Jy
вычисляют теоретическое
значение
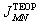 и сравнивают
его с экспериментальным (таб. 5.4).
и сравнивают
его с экспериментальным (таб. 5.4).
Таблица 5.4
Jx SJx Jz SJz JMN SJMN 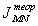
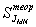
Подставляя в (5.13) определенные экспериментально геометрические размеры a, b, c и времена опускания груза tx , ty , tz , tAG для различных способов крепления тела в рамке, убеждаются в правильности (в пределах погрешности измерений) соотношения (5.13), а следовательно, и уравнения (5.5).
Рассмотрим малые колебания
физического маятника,
представляющего собой сложное тело,
состоящее из рамки, закрепленного
на стержне дополнительного
груза и исследуемого тела,
в качестве которого выбран
параллелепипед (рис.18) или
цилиндр (рис.19). Колебания
происходят вокруг оси,
проходящей через центр масс
рамки и исследуемого
тела. Действие моментов
сил тяжести, приложенных к
стержню и добавочному грузу,
закрепленному на нем, приводит к
возникновению колебаний всей системы.
Основное уравнение
вращательного движения
в этом случае имеет вид
 , (5.14)
, (5.14)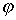 - угол
отклонения рамки от
положения равновесия,
m - масса груза,
l - расстояние от центра масс
груза до оси вращения,
m0 , l0
- масса и длина стержня, на котором
закреплен дополнительный груз,
J'=J+J0
момент инерции физического
маятника, включающего
в себя исследуемое тело (J) ,
рамку со стержнем
и дополнительным грузом (J0) .
- угол
отклонения рамки от
положения равновесия,
m - масса груза,
l - расстояние от центра масс
груза до оси вращения,
m0 , l0
- масса и длина стержня, на котором
закреплен дополнительный груз,
J'=J+J0
момент инерции физического
маятника, включающего
в себя исследуемое тело (J) ,
рамку со стержнем
и дополнительным грузом (J0) .
Уравнение (5.14) является уравнением собственных свободных колебаний
 (5.15)
(5.15)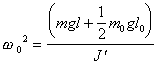 Так как
Так как
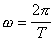 , то
, то
 (5.16)
(5.16)
Для момента
инерции исследуемого
тела относительно
фиксированной оси вращения
получаем:
J = J' - J0 , или
 (5.17)
(5.17)В частности, для параллелепипеда можно определить Jx , Jy , Jz для осей, совпадающих с главными центральными осями (рис.18), а также момент инерции относительно оси, совпадающей с одной из диагоналей параллелепипеда - например AG, выразив Jx , Jy , Jz , JAG в соответствии с (5.17) через периоды колебаний Tx , Ty , Tz , TAG и период колебаний пустой рамки T0.
Выразим момент
инерции тела относительно
оси AG в соответствии
с уравнением (5.9) через
Jx , Jy , Jz:
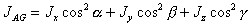
или
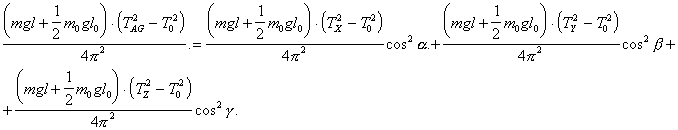
Учитывая, что сумма
квадратов направляющих
косинусов равна
единице, получаем

или
 (5.18)
(5.18)Рассмотривая колебания цилиндра относительно осей Oy, Oz, MN, можно найти величины Jy , Jz , JMN определяя, соответственно, периоды колебаний Ty , Tz , TMN .
Рассмотрим колебания
цилиндра относительно
оси MN (рис.19).
Направляющие косинусы для этой оси равны
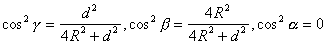 . (5.19)
. (5.19)
Момент инерции цилиндра
относительно оси MN ,
как и в предыдущем
уравнении, можно выразить
через компоненты тензора
инерции
Jy , Jz
, записанного
в главных осях (см.(5.5)):
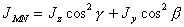 . (5.20)
. (5.20)Отметим, что уравнение (5.14) было записано без учета сил трения в оси маятника. Это обстоятельство, однако, практически не сказывается на уравнении (5.17), так как силы трения слабо влияют на период колебаний физического маятника.
Для выполнения работы необходимо измерить массы и размеры тел: радиус R и длину d цилиндра, ребра параллелепипеда а также массу груза m, массу и длину стержня m0 , l0. Рекомендуется проводить измерения каждой величины не менее трех раз, а линейных величин в различных сечениях тела. Данные заносят в табл. 5.5.
Таблица 5.5
Исследуемое
тело
ПараметрЦилиндр Параллепипед m m0 l0 N 1 2 3 1 2 3 R <R> , S<R> d <d> , S<d> a <a> , S<a> b <b> , S<b> c <c> , S<c> Дополнительный груз закрепляют в крайнем нижнем положении. Параллелепипед закрепляют в рамке в разных положениях и измеряют время tn, n=3-5 колебаний маятника. Для каждого положения тела проводят не менее трех измерений. Значения n и tn заносят в таблицу 5.6.
Характеристики колебательного движения параллелепипеда Таблица 5.6
N nx tnx Tx nz tnz Tz ny tny Ty nAG tnAG TAG Измеряют время tn0 3-5 колебаний рамки без тела. Измерения проводят не менее 3-х раз. Данные заносят в таблицу 5.7.
Характеристики колебательного движения цилиндра Таблица 5.7
N n0 tn0 T0 nz tnz Tz ny tny Ty nMN tnMN TMN Закрепляют в рамке цилиндр, измеряют времена tn для колебаний цилиндра относительно осей z, y, MN. Результаты заносят в таблицу 5.7.
Определяют средние арифметические значения и среднеквадратичные отклонения для размеров цилиндра и параллелепипеда и их погрешности. Результаты заносят в табл. 5.8.
Таблица 5.8
a , S a b , S b c , S c R , S R d , S d Находят средние значения периодов колебаний параллелепипеда Tx , Ty , Tz , TAG. Находят погрешности этих величин. Результаты заносят в табл. 5.9.
Таблица 5.9
<Tx> , S<Tx> <Ty> , S<Ty> <Tz> , S<Tz> <TAG> , S<TAG> Подставляют в (5.18) определенные экспериментально геометрические размеры и периоды колебаний маятника для различных способов крепления параллелепипеда в рамке. Находят ошибки определения величин, стоящих в правой и левой частях уравнения (5.18). Убеждаются в правильности равенства (5.18) в пределах ошибок измерений.
Таблица 5.10
<T0> , S<T0> <Ty> , S<Ty> <Tz> , S<Tz> <TMN> , S<TMN> Находят средние значения периодов колебаний цилиндра Ty , Tz , TMN и пустой рамки T0 и их погрешности. Результаты вносят в табл. 5.10. Определяют по формуле (5.17) значения моментов инерции Jy , Jz , JMN. для цилиндра. Находят погрешности этих величин. Результаты заносят в табл. 5.11.
Таблица 5.11
Jx SJx Jy SJy JMN SJMN ##### ##### Подставляя в (5.20) определенные в п.4 значения Jy , Jz , находят теоретическое значение момента инерции JMN , сравнивают его с экспериментальным (найденным в п.4).
В результате выполнения работы должно быть проверено соотношение (5.13) или (5.18) для цилиндра и проведено сравнение экспериментального и теоретического значений величины момента инерции при вращении тела относительно оси MN .
Контрольные вопросы
Записать уравнение моментов и объяснить смысл входящих в него величин
Какова связь между моментом импульса и угловой скоростью? Что такое тензор инерции.
Записать компоненты тензора инерции для простейших систем - тонкая палочка, система материальных точек.
Что такое главные оси? Что такое центральные оси. Примеры.
Как направлены векторы угловой скорости и момента количества движения при вращении тела вокруг закрепленной оси
1) если ось вращения совпадает с одной из главных осей.
2) если ось вращения не совпадает ни с одной из главных осей.
Связь между компонентами тензора инерции и моментом инерции относительно фиксированной оси .
Что такое эллипсоид инерции? Как определить значение момента инерции тела относительно заданной оси.
Алешкевич В.А., Деденко Л.Г., Караваев В.А. Механика твердого тела. Лекции (Университетский курс общей физики). М.: Изд-во физического факультета МГУ, 1998.
Сивухин Д.В. Общий курс физики. Том 1. Механика,3-е изд.: Наука.1989, § 53.