Цель работы
В работе испoльзуются
два способа экспериментального
определения момента инерции.
Первый основан на использовании
зависимости периода колебаний
физического маятника от его
момента инерции.Второй - на
анализе инерционных свойств
твердого тела, закрепленного
на оси, при его вращательном
движении. Кроме этого, проводится
прямой расчет момента инерции
исследуемого тела известной
геометрии.
Уравнение вращательного
движения для твердого
тела, закрепленного на
оси, имеет вид
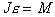 . (4.1)
. (4.1)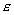 -
его угловое ускорение,
M- момент внешних сил, приложенных к телу.
-
его угловое ускорение,
M- момент внешних сил, приложенных к телу.
Величина момента инерции относительно какой-либо оси определяется пространственным распределением массы тела. В частности, для тела, состоящего из конечного числа элементарных (малых) масс mi .
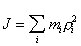 . (4.2)
. (4.2)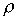 расстояние от элементарной массы
до оси вращения. В общем случае,
для сплошных тел, суммирование
заменяется интегрированием:
расстояние от элементарной массы
до оси вращения. В общем случае,
для сплошных тел, суммирование
заменяется интегрированием:
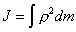
Для некоторых тел простой формы, возможен прямой расчет момента инерции. При сложной форме тела и неравномерном распределении его плотности аналитический расчет величины момента инерции может стать достаточно сложной задачей.
В данной работе применяются два способа экспериментального определения момента инерции: с помощью анализа колебаний физического маятника, составной частью которого является исследуемое тело, и с помощью изучения вращательного движения этого тела.
 Определение момента инерции твердого
тела на основе анализа его колебаний как физического маятника.
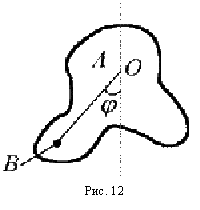
Если закрепить исследуемое
тело А на горизонтальной оси O,
проходящей через центр масс (рис.12),
то момент сил тяготения будет равен нулю,
и тело остается в состоянии безразличного
равновесия.
Если теперь закрепить на
исследуемом теле на некотором
удалении L
от оси малое тело В
с известной массой m,
то равновесие перестанет быть
безразличным - при равновесии
момент силы тяжести, действующий
на тело В будет равен нулю.
Такую систему тел можно
рассматривать как физический маятник.
Определение момента инерции твердого
тела на основе анализа его колебаний как физического маятника.
Если закрепить исследуемое
тело А на горизонтальной оси O,
проходящей через центр масс (рис.12),
то момент сил тяготения будет равен нулю,
и тело остается в состоянии безразличного
равновесия.
Если теперь закрепить на
исследуемом теле на некотором
удалении L
от оси малое тело В
с известной массой m,
то равновесие перестанет быть
безразличным - при равновесии
момент силы тяжести, действующий
на тело В будет равен нулю.
Такую систему тел можно
рассматривать как физический маятник.
Уравнение движения такого маятника имеет вид
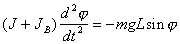 . (4.3)
. (4.3)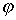 угол отклонения тела от положения
равновесия,
угол отклонения тела от положения
равновесия, 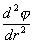 - его угловое ускорение.
- его угловое ускорение.
Если углы отклонения малы
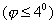 ,
то
,
то 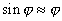 можно записать
можно записать
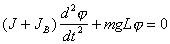 . (4.4)
. (4.4)Данное уравнение является уравнением собственных (свободных) гармонических колебаний, его решение имеет вид
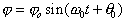 . (4.5)
. (4.5)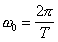 - собственная циклическая частота, T
-период колебаний,
- собственная циклическая частота, T
-период колебаний, 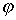 0
- амплитуда колебаний
0
- амплитуда колебаний
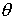 0 -начальная фаза колебаний.
0 -начальная фаза колебаний.
Дважды дифференцируя соотношение (4.5) по времени, получаем
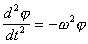 . (4.6)
. (4.6)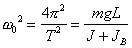 . (4.7)
. (4.7)В связи с тем, что размеры малого тела В во много раз меньше расстояния до оси L, можно считать его материальной точкой и положить
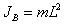 . (4.8)
. (4.8)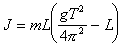 . (4.9)
. (4.9)Таким образом, для определения момента инерции твердого тела можно закрепить его на оси, проходящей через центр масс, установить на нем добавочное малое тело с известной массой, измерить период колебаний и зная расстояние L, по формуле (4.9) определить неизвестный момент инерции.
Отметим, что при выводе соотношения (4.9) не учитывалось влияние момента сил трения (Mтр ) в оси. Это приближение обусловлено тем, что при достаточно малом Mтр его воздействие приводит прежде всего к постепенному уменьшению амплитуды колебаний и практически не влияет на их период.
 Определение момента инерции
твердого тела на основе анализа
его равноускоренного вращательного движения.
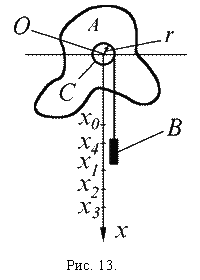
Рассмотрим, как и в предыдущем случае тело
А, закрепленное на оси O,
проходящей через центр масс (рис.13).
Соосно с телом закреплен цилиндр
С, на который наматывается
нить с прикрепленным к ней грузом
В.
Определение момента инерции
твердого тела на основе анализа
его равноускоренного вращательного движения.
Рассмотрим, как и в предыдущем случае тело
А, закрепленное на оси O,
проходящей через центр масс (рис.13).
Соосно с телом закреплен цилиндр
С, на который наматывается
нить с прикрепленным к ней грузом
В.
Под действием силы тяжести груз будет опускаться, приводя исследуемое тело А во вращение. Уравнение движения груза В, уравнение вращательного движения тела А и уравнение кинематической связи имеют вид
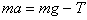 . (4.10)
. (4.10)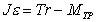 . (4.11)
. (4.11)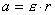 . (4.12)
. (4.12)Из уравнений (4.10) -(4.12) получаем
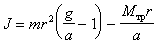 . (4.13)
. (4.13)Предположим, что груз начинает опускаться с отметки x0=0, а мы измеряем время
 t
прохождения его между двумя точками
x0 и x1.
Движение грузика в участке
x1-x2.
является равноускоренным,
и можно записать
t
прохождения его между двумя точками
x0 и x1.
Движение грузика в участке
x1-x2.
является равноускоренным,
и можно записать
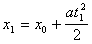 . (4.14)
. (4.14)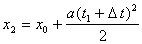 . (4.15)
. (4.15) t
- время прохождения участка
x2-x1.
t
- время прохождения участка
x2-x1.
Из (4.14) и (4.15) следует:
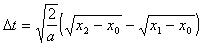 . (4.16)
. (4.16)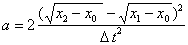 . (4.17)
. (4.17)Таким образом, для определения a нам нужно знать x0,x1,x2 и время
 t прохождения
грузика между точками с координатами
x1 и x2.
t прохождения
грузика между точками с координатами
x1 и x2.
Рассмотрим соотношения, позволяющие определить момент сил трения. При опускания груза с отметки x0 на полную длину нити до отметки x3 его потенциальная энергия переходит в кинетическую и в некоторое количество тепловой энергии, по величине равное работе сил трения,
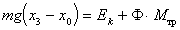 . (4.18)
. (4.18)После того, как груз опустится на полную длину нити до отметки x3 , тело будет продолжать вращаться, и нить начнет наматываться на цилиндр. В результате груз поднимется до отметки x4. Очевидно,
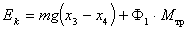 . (4.19)
. (4.19)Учитывая, что
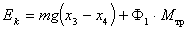 , получаем величину момента силы трения
, получаем величину момента силы трения
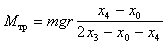 . (4.20)
. (4.20)
Установка представляет собой
сплошное колесо (рис. 14),
которое может вращаться вокруг
горизонтальной оси
(
для упражнения 1
AVI (2.6M)
и
для упражнения 2
AVI (5.5M)
). К цилиндру,
расположенному на оси колеса, с помощью
нити прикреплен груз.
Помещая груз в
устройство для его крепления,
получаем физический маятник, который
может колебаться около положения
равновесия. Угол отклонения может
быть определен по
угломерной шкале.
В том случае, когда груз
освобожден (при этом устройство
для его крепления снимается с колеса),
под действием силы тяжести он начнет
опускаться, приводя колесо во вращение.
Установка снабжена системами регистрации
периода колебаний колеса и времени
опускания груза.
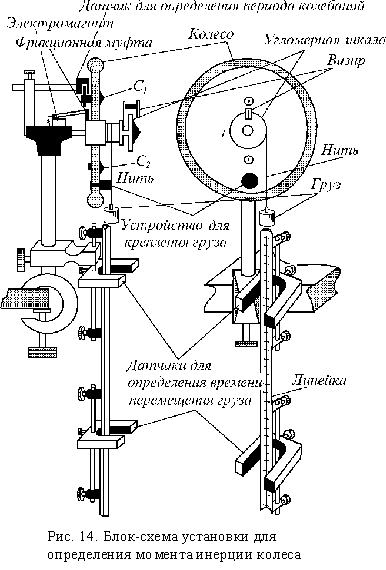
Для регистрации периода
колебаний на колесе
симметрично расположены
два легких одинаковых по массе тела
C1 и C2 .
На теле C1
закреплен стержень, являющийся
составной частью системы
измерения периода колебаний.
В исходном положении система
зафиксирована с помощью
фрикционной муфты,
управляемой электромагнитом
( при таком положении муфты
светится лампа индикации на
кнопке управления электромагнитом).
При выключении электромагнита фрикционная
муфта освобождает колесо, и оно начинает
движение (колебательное или вращательное).
Время колебаний колеса определяется с
помощью электронного таймера. Время
перемещения груза при вращательном
движении колеса определяется с помощью
того же таймера, включение и выключение
которого в этом случае осуществляется
оптическими датчиками.
Эти датчики крепятся на кронштейнах
и могут фиксироваться на различных
высотах. Положение датчиков
определяется с помощью
линейки (рис.14)
Запуск таймера в режиме
измерения периодов колебаний
осуществляется нажатием кнопки
"Пуск", остановка - кнопкой
"Стоп". При измерении времени
опускания груза нажимают на кнопку
"Пуск", после чего на индикаторе
электронного таймера высвечивается
время прохождения груза между двумя
датчиками положения. Переключение
таймера в тот или иной режим
работы осуществляется тумблером
"Колеб.- Вращ.". При подготовке
к дальнейшим измерениям
результаты предыдуших убираются
с табло нажатием кнопки "Сброс".
Упражнение 1. Определение момента инерции колеса методом колебаний.
На краю колеса закрепляют устройство для крепления груза, в которое устанавливают груз, колесо выводят из положения равновесия на угол, не превышающий 100. Определяют время tn полных колебаний n=10 : 15. Такое измерение проводят 3-5 раз. Результаты измерений времени заносятся в табл.4.1.
После этого не менее трех раз измеряют расстояние L от оси вращения до центра масс груза ( это есть расстояние от оси вращения до центра винта, закрепляющего устройство крепления груза на колесе). Результаты заносятся в табл.4.1.
Взвешивают устройство для крепления груза и сам груз. Значения масс тел mк и mгр заносят в табл.4.1.
Таблица 4.1
| N | n | tn | TN | < T > | ST | LN | < L > | SL | mк , mг | J | SJ |
| 1 | |||||||||||
| 2 | |||||||||||
| 3 | |||||||||||
| 4 | |||||||||||
| 5 |
По экспериментальным данным вычислить выборочные средние значения (средние арифметические значения) величин периода Т и расстояния L.
Вычислить выборочные стандартные отклонения (среднеквадратичные ошибки среднего арифметичсекого) для Т и L
По полученным данным, пользуясь уравнением (4.9) и учитывая, что m=mк+mгр, определяют момент инерции колеса J.
Оценить погрешности для J, используя следующую формулу для расчета погрешностей косвенных измерений:
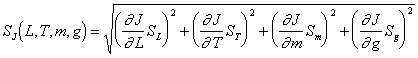 . (4.21)
. (4.21)Снять с колеса устройство для крепления груза.
Измерить время
 t
прохождения груза между
отметками x1
и x2.
Измерения провести не менее
5-7 раз для фиксированных
значений x0,x2
и разных x1,
каждый раз занося данные
в табл.4.2. Измеряют
также координату x3
точки, до которой опускается груз при
полностью размотанной нити и координату
x4
точки, до которой поднимается
груз при дальнейшем наматывании
нити на цилиндр, пока колесо
продолжает свободно вращаться.
t
прохождения груза между
отметками x1
и x2.
Измерения провести не менее
5-7 раз для фиксированных
значений x0,x2
и разных x1,
каждый раз занося данные
в табл.4.2. Измеряют
также координату x3
точки, до которой опускается груз при
полностью размотанной нити и координату
x4
точки, до которой поднимается
груз при дальнейшем наматывании
нити на цилиндр, пока колесо
продолжает свободно вращаться.
Несколько раз измерить радиус r цилиндра, на который наматывается нить.
Таблица 4.2
| N | x1 | x2 | #t | aN | < a > | Sa | x0 | x3 | x4 | Mтр | < M > | SM |
| 1 | ||||||||||||
| 2 | ||||||||||||
| 3 | ||||||||||||
| .... | ||||||||||||
По формулам (4.17) и (4.20) определить ускорения aN и моменты сил трения Mтр для каждого измерения. Результаты измерений заносятся в табл.4.2.
Поскольку aN и Mтр определяются для различных значений x1, то будем считать полученные значения ускорений и моментов сил трения независимыми. Найти выборочные средние значения ускорения и момента сил трения и выборочные стандартные отклонения этих величин. Результаты вычислений занести в табл.4.2.
Вычислить выборочное среднее значение радиуса < r > цилиндра и среднеквадратичную ошибку этой величины.
По формуле (4.13 ) определить значение момента инерции колеса и его погрешность.
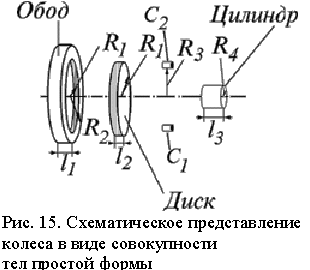 Используемое в установке
колесо можно представить
как совокупность тел простой
формы (рис.15), диска радиуса R1,
толщины l1 ; обода толщины
l2
с внешним и внутренним радиусами
R2,R1;
двух малых тел
C1 и C2,
расположенных на расстоянии
R3 от оси;
цилиндра, имеющего радиус
R4 и толщину
l3.
Для всех этих тел момент
инерции можно рассчитать.
Используемое в установке
колесо можно представить
как совокупность тел простой
формы (рис.15), диска радиуса R1,
толщины l1 ; обода толщины
l2
с внешним и внутренним радиусами
R2,R1;
двух малых тел
C1 и C2,
расположенных на расстоянии
R3 от оси;
цилиндра, имеющего радиус
R4 и толщину
l3.
Для всех этих тел момент
инерции можно рассчитать.
Известно, что момент инерции диска массы mд относительно оси равен (см. Приложение 4)
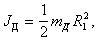 . (4.22)
. (4.22)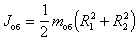 . (4.23)
. (4.23)Учитывая, что диск, обод и цилиндр сделаны из одного материала с плотностью
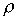 , получаем окончательно выражение
для момента инерции колеса
, получаем окончательно выражение
для момента инерции колеса
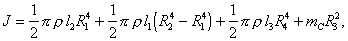 . (4.24)
. (4.24)С помощью штангенциркуля и линейки определяют геометрические размеры каждой выделенной части колеса по несколько раз. Результаты измерений заносят в таблицу 4.3.
Таблица 4.3
| N | 1 | 2 | 3 | 4 | 5 |
| R 1n | |||||
| < R 1 > | |||||
| S R 1 | |||||
| R 2n | |||||
| < R 2 > | |||||
| S R 2 | |||||
| R 3n | |||||
| < R 3 > | |||||
| S R 3 | |||||
| R 4n | |||||
| < R 4 > | |||||
| S R 4 | |||||
| N | 1 | 2 | 3 | 4 | 5 |
| l 1n | |||||
| < l 1 > | |||||
| S l 1 | |||||
| l 2n | |||||
| < l 2 > | |||||
| S l 2 | |||||
| l 3n | |||||
| < l 3 > | |||||
| S l 3 | |||||
Определяют средние арифметические значения R1,R2,R3,R4, l1,l2,l3. Результаты заносят в таблицу 4.3.
Вычисляют выборочные стандартные отклонения для этих величин. Результаты заносят в таблицу 4.3.
По формуле (4.24) рассчитывают значение момента инерции колеса и определяют погрешность.
Рассчитанное значение момента инерции колеса сравнивают с значениями, полученными экспериментально в упражнениях 1 и 2.
В процессе выполнения работы должен быть определен момент инерции колеса двумя способами. Следует сопоставить эти результаты с величиной вычисленного по (4.24) момента инерции.
Контрольные вопросы
Что такое главные оси инерции? Центральные оси? Привести примеры.
Что такое момент инерции тела относительно закрепленной оси?
Чему равны моменты инерции следующих тел: тонкая палочка, тонкий диск, тонкие прямоугольная и треугольная пластины, цилиндр, шар, параллелепипед? Как их получить?
Сформулируйте теорему Гюйгенса-Штейнера.
Алешкевич В.А., Деденко Л.Г., Караваев В.А. Механика твердого тела. Лекции (Университетский курс общей физики). М.: Изд-во физического факультета МГУ, 1998.
Сивухин Д.В. Общий курс физики. Том 1. Механика,3-е изд.: Наука.1989, гл V.