Цель работы
состоит в изучении свободных
колебаний системы имеющей две
степени свободы, являющейся
частным случаем системы с
несколькими степенями свободы.
Рассматриваются два математических
маятника, связанных между собой
пружиной. Дополнительное устройство
позволяет возбуждать любое из двух
нормальных колебаний, а также колебание,
являющееся суперпозицией нормальных.
Характеристики колебательной системы
определяются из ее геометрии, измеренных
периодов нормальных колебаний и периода биений.
Многие колебательные системы представляют собой системы двух или нескольких связанных между собой осцилляторов. Примерами могут служить молекулы (атомы, взаимодействующие между собой), маятники, колеблющиеся вокруг одной оси (связь осуществляется посредством упругих сил в оси), связанные электрические контуры. Особенности колебаний в таких системах рассмотрим на примере двух математических или физических маятников, связанных между собой пружиной.
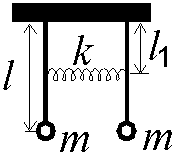 Свободный математический маятник, как известно, обладает двумя степенями свободы, то есть для описания его движения требуется два параметра - углы смещения в двух взаимно перпендикулярных плоскостях.
Свободный математический маятник, как известно, обладает двумя степенями свободы, то есть для описания его движения требуется два параметра - углы смещения в двух взаимно перпендикулярных плоскостях.
Система из двух маятников описывается четырьмя параметрами и, следовательно, имеет четыре степени свободы. Если колебания, соответствующие каждой степени свободы, независимы, то задача описания движения является чисто кинематической, то есть задачей разложения сложного движения на сумму более простых движений. Если между движениями по различным степеням свободы имеется динамическая связь, при которой возбуждение одной степени свободы вызывает динамические изменения во всех остальных степенях свободы, то это приводит к обмену колебательной энергии между степенями свободы, приводя к новым физическим явлениям, отсутствующим у системы независимых маятников.
В настоящей лабораторной работе изучаются колебания системы из двух связанных одинаковых маятников, имеющей только две степени свободы (рис1). Для этого подвес каждого маятника осуществляется при помощи маленьких подшипников, обладающих малым трением, которые позволяют маятникам двигаться только в вертикальной плоскости, проходящей через линию, соединяющую точки подвеса.
Как известно, для свободного математического маятника уравнение моментов будет
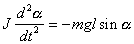 (1)
(1) - угол отклонения от положения равновесия.
- угол отклонения от положения равновесия.
В случае двух маятников, связанных пружиной, на каждый маятник будет действовать дополнительная сила со стороны пружины Fсв, которая при небольших отклонениях может быть определена из закона Гука ,
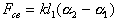
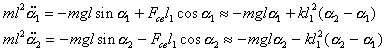 (2)
(2)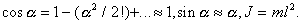
В общем случае уравнения колебаний в системе двух произвольных связанных маятников имеют вид
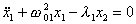 (3)
(3)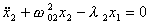 (4)
(4)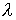 1 ,
1 , 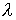 2
- коэффициенты, определяющие величину связи между маятниками.
2
- коэффициенты, определяющие величину связи между маятниками.
Как следует из (2)-(4) для рассматриваемого случа
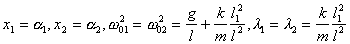 (5)
(5)Решение системы (3),(4) легко найти с помощью метода комплексных амплитуд, если предположить, что в ней можно возбудить гармонические колебания на некоторой частоте w, причем
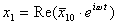 (6)
(6)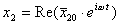
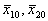 - комплексные амплитуды колебаний маятников.
- комплексные амплитуды колебаний маятников.
После подстановки (6) в (3), (4) получим
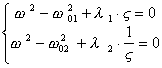 (7)
(7)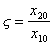 . Решением этой системы алгебраических уравнений являются
. Решением этой системы алгебраических уравнений являются
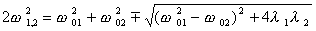 (8)
(8)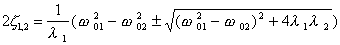 (9)
(9)Здесь верхний знак перед корнем относится к w1 и
 1 , а нижний - к
w2 и
1 , а нижний - к
w2 и
 2 .
2 .
Общее решение системы (3), (4) имеет вид
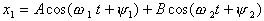 (10)
(10)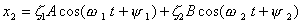 (11)
(11)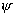 1 ,
1 , 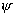 2
определяются начальными условиями, а частоты
w1 , w2
и коэффициенты
2
определяются начальными условиями, а частоты
w1 , w2
и коэффициенты
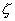 1 ,
1 , 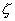 2
не зависят от начальных условий и определяются только свойствами колебательной
системы. Для случая двух одинаковых связанных маятников из (9) следует
2
не зависят от начальных условий и определяются только свойствами колебательной
системы. Для случая двух одинаковых связанных маятников из (9) следует
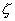 1 = 1 ,
1 = 1 , 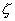 2 = -1 .
2 = -1 .
Таким образом, хотя в общем случае произвольное колебание маятников не является гармоническим, тем не менее его всегда можно представить в виде суммы двух гармонических колебаний с частотами w1 и w2 . Эти колебания носят название нормальных колебаний (собственных колебаний системы), а частоты w1 и w2 - нормальных частот. Каждое нормальное колебание системы ( его называют также модой колебаний) является совокупностью колебаний обоих маятников, оно характеризуется частотой w1 или w2 , а также определенным соотношением между амплитудами колебаний каждого маятника( амплитуды отличаются соответственно в
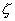 1 или
1 или 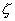 2 раз).
2 раз).
Нормальные колебания можно выделить в любой колебательной системе, состоящей из произвольного числа маятников, если движение этой системы описывается системой уравнений типа (3), (4). В том случае, когда в системе возбуждено одно нормальное колебание, каждый маятник колеблется по гармоническому закону с частотой этого колебания, а амплитуды и фазы колебаний всех входящих в систему маятников однозначно связаны между собой.
Рассмотрим основные положения, выявленные при анализе колебаний в системе из двух связанных маятников.
Число парциальных частот равно числу нормальных частот и равно числу степеней свободы в рассматриваемой системе.
Парциальные частоты w01 и w02 лежат между нормальными частотами w1 и w2 .
Характер взаимодействия маятников определяется подкоренным выражением в (8), (9), то есть величиной отношения
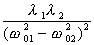 , которая называется связанностью.
, которая называется связанностью.
В случае малой связанности нормальное колебание с частотой w1 характеризуется возбуждением прежде всего первого маятника системы с частотой, близкой к w01 (
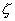 1
1 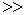 1 и x01
1 и x01 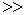 x02 ) .
Другое нормальное колебание характеризуется преимущественным возбуждением второго маятника.
x02 ) .
Другое нормальное колебание характеризуется преимущественным возбуждением второго маятника.
В предельном случае сильной связанности, когда, например, w01 = w02 = w0 , энергия каждого нормального колебания равномерно распределена между отдельными системами, т.е. маятники колеблются с близкими амплитудами (
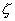 1 = -
1 = -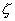 2 ),
а нормальные частоты равны
2 ),
а нормальные частоты равны
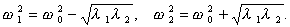
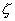 1 = 1 ,
1 = 1 ,
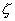 2 = -1 получаем из (10), (13)
2 = -1 получаем из (10), (13)
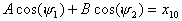
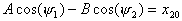
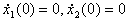 (13)
(13)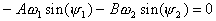
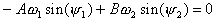
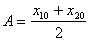 (14)
(14)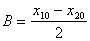 (15)
(15)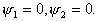 (16)
(16)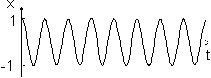 В том случае, когда x10 = x20
(в начальный момент маятники смещены в одну сторону),
в системе возбуждается одно нормальное колебание с
частотой w1 (
В том случае, когда x10 = x20
(в начальный момент маятники смещены в одну сторону),
в системе возбуждается одно нормальное колебание с
частотой w1 ( 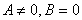 ).
Зависимость смещения каждого маятника от времени имеет вид (рис.2а):
).
Зависимость смещения каждого маятника от времени имеет вид (рис.2а):
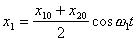
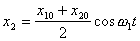
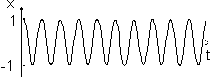 Так как эти зависимости одинаковы, то такие колебания называются синфазными.
Так как эти зависимости одинаковы, то такие колебания называются синфазными.
Если x10 = -x20 ( маятники в начале отклонены в разные стороны), то
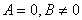 , и зависимости смещения от времени имеют вид, показанный на рис.3, так как выполняются соотношения
, и зависимости смещения от времени имеют вид, показанный на рис.3, так как выполняются соотношения
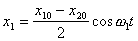
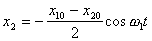
В общем случае в системе одновременно возбуждаются оба нормальных колебания. Рассмотрим частный случай, когда, например,
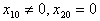 .
В этом случае
.
В этом случае 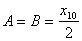 .
Законы движения для каждого маятника имеют вид.
.
Законы движения для каждого маятника имеют вид.
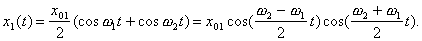 (17)
(17)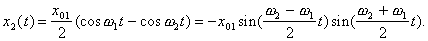 (18)
(18)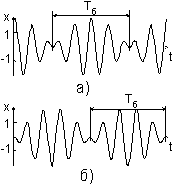 Зависимости смещения от времени имеют вид,
показанный на рис.2 в,г. Считая, как в нашем случае, что
Зависимости смещения от времени имеют вид,
показанный на рис.2 в,г. Считая, как в нашем случае, что
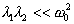 , получаем, что
w1
, получаем, что
w1 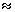 w2 и
w2 и
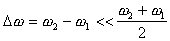 .
В этом случае (15) и (16) описывают
так называемые биения двух близких
частот, то есть x1 (t) и
x2 (t)
мы можем рассматривать как колебания,
происходящие с периодом
.
В этом случае (15) и (16) описывают
так называемые биения двух близких
частот, то есть x1 (t) и
x2 (t)
мы можем рассматривать как колебания,
происходящие с периодом
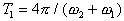 , амплитуда которых медленно
( по отношению к T1) меняется
со временем по закону
, амплитуда которых медленно
( по отношению к T1) меняется
со временем по закону
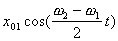 с периодом
с периодом 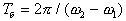 ( период биений -время между двумя моментами, когда амплитуда обращается в ноль).
( период биений -время между двумя моментами, когда амплитуда обращается в ноль).
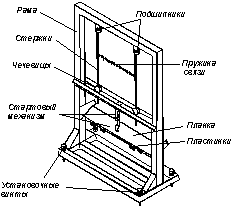 Установка состоит из деревянной ( рис.5)
рамы с установочными винтами
, на которой подвешены два одинаковых маятника.
Маятники состоят из длинных легких стержней,
на нижнем конце которых укреплены массивные
чечевицы. Верхние концы стержней
укреплены во внутренние шайбы подшипников,
внешние шайбы которых крепятся в раме таким
образом, чтобы плоскость подшипников,
а, следовательно, и плоскость движения
маятников совпадала с плоскостью рамы.
На расстоянии l1
от точки подвеса ( центра подшипника)
закреплена пружина связи,
длина которой в нерастянутом состоянии
точно равна расстоянию между стержнями
маятников в не отклоненном положении.
Ниже маятников установлен специальный
стартовый механизм,
который позволяет плавно запускать
маятник при различных начальных отклонениях
от положения равновесия. Он состоит из
поворачивающейся планки, на которой в разных
положениях устанавливаются небольшие пластинки,
которые удерживают концы маятников
в заданных отклоненных положениях. При повороте планки
пластинки поворачи ваются вместе с ней,
освобождая концы маятников, которые начинают совершать колебания.
Установка состоит из деревянной ( рис.5)
рамы с установочными винтами
, на которой подвешены два одинаковых маятника.
Маятники состоят из длинных легких стержней,
на нижнем конце которых укреплены массивные
чечевицы. Верхние концы стержней
укреплены во внутренние шайбы подшипников,
внешние шайбы которых крепятся в раме таким
образом, чтобы плоскость подшипников,
а, следовательно, и плоскость движения
маятников совпадала с плоскостью рамы.
На расстоянии l1
от точки подвеса ( центра подшипника)
закреплена пружина связи,
длина которой в нерастянутом состоянии
точно равна расстоянию между стержнями
маятников в не отклоненном положении.
Ниже маятников установлен специальный
стартовый механизм,
который позволяет плавно запускать
маятник при различных начальных отклонениях
от положения равновесия. Он состоит из
поворачивающейся планки, на которой в разных
положениях устанавливаются небольшие пластинки,
которые удерживают концы маятников
в заданных отклоненных положениях. При повороте планки
пластинки поворачи ваются вместе с ней,
освобождая концы маятников, которые начинают совершать колебания.
Масса чечевиц маятников m,
эффективная длина l
( расстояние от точки подвеса
до центра чечевицы) и расстояние
l1 известны, их величины указаны на каждой установке.
Упражнение 1. Определение частот нормальных колебаний
Измерения
Определяют периоды колебаний каждого маятника в отдельности ( периоды парциальных колебаний). Для этого, не снимая пружины связи, возбуждают колебания одного маятника, удерживая при этом другой. С помощью секундомера определяют время пятидесяти колебаний каждого маятника и вычисляют период T01 и T02. Меняя положение чечевицы одного из маятников добиваются того, чтобы эти периоды были одинаковыми ( можно считать, что периоды равны, если ( T02 - T01 )/T01 меньше чем 0.01 ). После этого величину
T0 = T01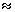 T02
заносят в табл.1.
T02
заносят в табл.1.
Сначала отклоняют маятники в одну сторону и фиксируют их с помощью стартового механизма. Такие начальные условия соответствуют возбуждению синфазных колебаний с частотой w1. Запускают движение маятников, убеждаются, что оно является гармоническим. При помощи секундомера определяют время 20-30 колебаний первого маятника, данные записывают в табл.1. Измерения проделывают не менее трех раз.
Устанавливают начальные условия для возбуждения противофазных колебаний, для этого отклоняют маятники на одинаковый угол в противоположных направлениях и фиксируют их с помощью стартового механизма. Возбуждают колебания. Определяют с помощью секундомера время 20-30 колебаний, данные записывают в табл. 1. Измерения проделывают не менее трех раз.
Определяют частоту собственных колебаний маятников w0.
Определяют период синфазных ( T1 ) и противофазных колебаний ( T2 ) и погрешность их определения. Данные заносят в табл.1.
Зная периоды синфазных и противофазных колебаний определяют нормальные частоты w1 и w2 и погрешности их определения.
Сравнивают между собой величины ( w1 + w2 ) и 2w0 . В соответствии с (8) эти величины должны быть равны с учетом погрешности эксперимента.
Таблица 1
| номер опыта | n (синфазные колеб.) | tn | T1 , ST1 | n (проти-вофазн. колеб.) | tn | T2 , ST2 | w1 , Sw1 | w2 , Sw2 |
| 1 | ||||||||
| 2 | ||||||||
| 3 |
Измерения
С помощью стартового механизма реализуют такие начальные условия, когда один маятник в начале отклонен, а второй находится в положении равновесия. Возбуждают колебания. С помощью секундомера определяют период биений Tб - время между двумя последовательными моментами, когда амплитуда первого маятника обращается в ноль. Данные заносят в табл2. Измерения проводят не менее трех раз.
Определяют средние значения периода Tб и частоты wб биений и погрешность их измерения
Определяют теоретическое значение частоты биений по формуле (
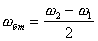 ) и сравнивают его
с найденным экспериментально. Выполнение
равенства
wб = wбт
косвенным образом подтверждает, что сложный колебательный процесс в системе сводится к сумме двух нормальных колебаний.
) и сравнивают его
с найденным экспериментально. Выполнение
равенства
wб = wбт
косвенным образом подтверждает, что сложный колебательный процесс в системе сводится к сумме двух нормальных колебаний.
Таблица 2
| номер опыта | Tбi | Tб , STб | wб , Swб | wбт , Swбт |
| 1 | ||||
| 2 | ||||
| 3 |
В процессе выполнения работы необходимо убедиться, что в системе с двумя степенями свободы можно возбудить два нормальных колебания, происходящие по гармоническому закону. Должны быть определены частоты этих колебаний. Необходимо убедиться, что в общем случае колебания системы с двумя степенями свободы не являются гармоническими. Определяя период биений для частного случая косвенным образом убеждаются, что произвольное колебание является суперпозицией нормальных колебаний.
Контрольные вопросы
Что такое моды колебаний системы, нормальные частоты, парциальные частоты?
Сколько нормальных колебаний может быть у системы с N степенями свободы?
Что такое связанность системы. Какой связанностью характеризуется рассмотренная система сильной или слабой?
Что такое биения? В каких случаях они наблюдаются?
В.А. Алешкевич, Л.Г. Деденко, В.А. Караваев. Университетский курс общей физики. Колебания и волны. Лекция 3.
Матвеев А.Н. Механика и теория относительности. 2-е изд. М.: Высшая школа, 1986, гл.13,п. 55.