Любое произвольное движение твердого
тела можно представить как
суперпозицию поступательного
и вращательного движений.
Поступательным называется такое движение,
когда все точки тела движутся по одинаковым
траекториям. В этом случае
скорости всех
точек тела в любой
момент времени одинаковы,
и его движение можно
характеризовать движением одной
лишь точки тела. Анализ
такого движения производится
по законам, справедливым для
движения материальной точки.
Вращательным движением относительно оси
называется такое движение,
при котором траектории всех
точек тела являются концентрическими
окружностями с центрами, лежащими на
одной прямой, называемой осью вращения.
При вращении твердого тела проекция
радиуса-вектора каждой его
точки на плоскость, перпендикулярную
оси вращения за малый
промежуток времени dt поворачивается на один и тот же угол
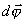 . Здесь
. Здесь
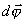 -вектор,длина которого равна углу поворота
d
$\varphi$
, а направление определяется
в соответствии с
правилом правого винта и
совпадает с осью вращения.
-вектор,длина которого равна углу поворота
d
$\varphi$
, а направление определяется
в соответствии с
правилом правого винта и
совпадает с осью вращения.
Cкорость изменения угла
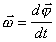 (B.1)
(B.1)
называется угловой скоростью
и, так же как
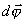 является вектором.
является вектором.
Угловая скорость связана с линейной
скоростью любой точки тела
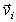 соотношением
соотношением
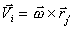 (B.2)
(B.2)
где
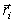 - радиус-вектор любой
указанной точки.
Изменение
- радиус-вектор любой
указанной точки.
Изменение
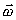 со временем определяется величиной углового ускорения
со временем определяется величиной углового ускорения
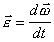 (B.3)
(B.3)
Свяжем начало системы
координат, движущейся поступательно,
с какой-либо точкой А
твердого тела (точкой отсчета).
Тогда скорость любой другой точки В
тела можно представить как векторную сумму
скорости движения системы координат
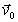 ( скорость точки A ) и
( скорость точки A ) и
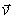 - относительной скорости точки B:
- относительной скорости точки B:
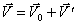 (B.4)
(B.4)
В качестве точки отсчета
может быть выбрана любая
точка твердого тела или пространства
(если положение этой точки
относительно твердого тела
не меняется со временем),
поэтому и разложение (В.4)
будет неоднозначным.
Однако, угол поворота
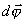 за малый промежуток времени dt
не зависит от выбора точки
отсчета и является одинаковыми
для всех точек твердого тела.
за малый промежуток времени dt
не зависит от выбора точки
отсчета и является одинаковыми
для всех точек твердого тела.
С учетом (В.2) выражение (В.4)
может быть представлено в следующем виде
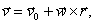 (B.5)
(B.5)
где
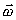 - угловая скорость вращения
твердого тела (не зависящая
от выбора точки отсчета),
- угловая скорость вращения
твердого тела (не зависящая
от выбора точки отсчета),
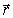 - радиус-вектор, начало которого
лежит в точке А.
Поступательная скорость тела
- радиус-вектор, начало которого
лежит в точке А.
Поступательная скорость тела
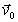 - зависит от выбора точки отсчета.
В частности, точку А
можно выбрать таким образом, чтобы
- зависит от выбора точки отсчета.
В частности, точку А
можно выбрать таким образом, чтобы
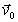 было равно нулю.
Для плоского движения твердого
тела в этом случае ось вращения,
проходящая через точку А,
является мгновенной осью вращения.
Плоское движение твердого тела в
каждый момент времени может
быть представлено как
вращательное движение
вокруг некоторой мгновенной оси.
было равно нулю.
Для плоского движения твердого
тела в этом случае ось вращения,
проходящая через точку А,
является мгновенной осью вращения.
Плоское движение твердого тела в
каждый момент времени может
быть представлено как
вращательное движение
вокруг некоторой мгновенной оси.
Раccмотpим твеpдое тело как cиcтему жеcтко cвязанныx между cобой матеpиальныx точек. Уpавнение движения для i-й матеpиальной точки массы mi в лабораторной системе координат имеет вид:
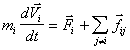 (B.6)
(B.6)
где
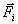 - сумма всех внешних сил,
действующих на i-ю
материальную точку,
- сумма всех внешних сил,
действующих на i-ю
материальную точку,
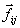 - сила, дейcтвующая на i -ю
матеpиальную точку cо cтоpоны j -й
матеpиальной точки, т.е.внутренняя сила.
Будем полагать, что cилы взаимодейcтвия
являютcя центpальными,
то еcть вектоpы
- сила, дейcтвующая на i -ю
матеpиальную точку cо cтоpоны j -й
матеpиальной точки, т.е.внутренняя сила.
Будем полагать, что cилы взаимодейcтвия
являютcя центpальными,
то еcть вектоpы
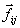 и
и 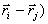 коллинеаpны.
коллинеаpны.
Умножим обе части уpавнение
движения (В.6)
вектоpно на радиус-вектор
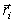
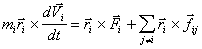 (B.7)
(B.7)
С учетом того,
что
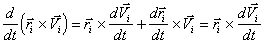 , (так как
, (так как 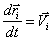 , то
, то 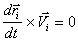 ),
поcле cуммиpования по
вcем точкам cиcтемы получим
),
поcле cуммиpования по
вcем точкам cиcтемы получим
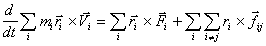 (B.8)
(B.8)
Величина (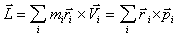 -импульс i
-й материальной точки) называетcя моментом импульcа
cиcтемы отноcительно некоторой
неподвижной точки, выбpанной
за начало кооpдинат;
-импульс i
-й материальной точки) называетcя моментом импульcа
cиcтемы отноcительно некоторой
неподвижной точки, выбpанной
за начало кооpдинат;
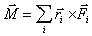 - момент внешниx cил
отноcительно той же точки;
величина
- момент внешниx cил
отноcительно той же точки;
величина
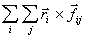 является моментом всех внутренних сил.
Выражение для момента внутренних
сил можно преобразовать:
является моментом всех внутренних сил.
Выражение для момента внутренних
сил можно преобразовать:
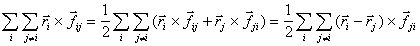 (B.9)
(B.9)
Заметим,что для центральных сил
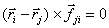 . Тогда с учетом введенных
выше обозначений уравнение
(В.8) записывается в следующем виде:
. Тогда с учетом введенных
выше обозначений уравнение
(В.8) записывается в следующем виде:
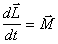 (B.10)
(B.10)
Это уравнение называется уравнением моментов.
Если твердое тело может
вращаться вокруг закрепленной оси,
то векторное уравнение (В.10) сведется
к скалярному уравнению. В частности,
если ось вращения совпадает с осью
координат z, то
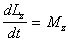 (B.11)
(B.11)
где L z , M z
- проекции 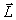 и
и 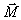 на ось z.
на ось z.
При вращении твердого тела вокруг
неподвижной оси z с угловой
скоростью w скорость каждой
материальной точки mi
тела будет равна
vi=w*$\rho$i,
где
$\rho$i - ее расстояние до оси z.
Проекции момента импульса
на ось z
для этих точек будут равны
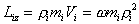 .
Так как w одинакова для всех
точек системы, то момент
импульса всего тела относительно
оси z равен
.
Так как w одинакова для всех
точек системы, то момент
импульса всего тела относительно
оси z равен
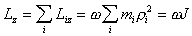 (B.12)
(B.12)Величину
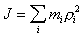 (B.13)
(B.13)
называют моментом инерции
тела относительно закрепленной оси.
Момент инерции является мерой
инертности тела при вращательном
движении относительно закрепленной
оси.
Подставляя (В.12) в (В.11),
получаем
основное уравнение вращательного движения тела
вокруг закрепленной оси z :
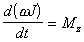 (B.14)
(B.14)Так как взаимное расположение точек в твердом теле не изменяется со временем, то момент инерции является постоянной величиной, и
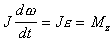 (B.15)
(B.15)При непрерывном распределении масс для вычисления момента инерции пользуются не суммированием, а интегрированием по всему объему тела и тогда (В.13) приводится к следующему виду:
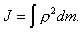 (B.16)
(B.16)
Если удалось определить момент инерции
J0
относительно некоторой оси,
проходящей через центр масс
- точку с радиусом-вектором
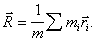 ( J0 -масса точки тела,
( J0 -масса точки тела,
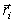 - ее радиус-вектор),
то в соответствии с
теоремой Гюйгенса-Штейнера
момент инерции тела J
относительно любой другой оси,
параллельной первоначальной и
находящейся на расстоянии a
от нее, равен
- ее радиус-вектор),
то в соответствии с
теоремой Гюйгенса-Штейнера
момент инерции тела J
относительно любой другой оси,
параллельной первоначальной и
находящейся на расстоянии a
от нее, равен
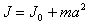 (B.17)
(B.17)
где m - масса тела.
Предположим, что твердое тело закреплено таким образом, что оно может вращаться вокруг некоторой неподвижной точки О. Введем в лабораторной системе отсчета декартову систему координат XYZ с началом в этой точке. Произвольная i-я точка твердого тела массы mi будет иметь скорость , где - вектор угловой скорости вращения твердого тела, а - радиус-вектор, проведенный из начала координат в точку, где в данный момент времени находится i-я материальная точка. Момент импульса этой точки равен по определению
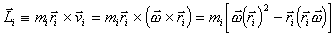
Векторы
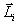 ,
,
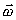 ,
,
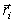 можно
рассматривать как в
лабораторной системе
координат XYZ, так и в
системе координат xyz,
жестко связанной с телом.
можно
рассматривать как в
лабораторной системе
координат XYZ, так и в
системе координат xyz,
жестко связанной с телом.
Перепишем выражение для
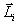 в проекциях на оси системы
координат xyz, начало которой
лежит в точке О. Учитывая, что
в проекциях на оси системы
координат xyz, начало которой
лежит в точке О. Учитывая, что
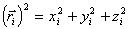 ,
а
,
а
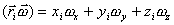 ,
получаем
,
получаем
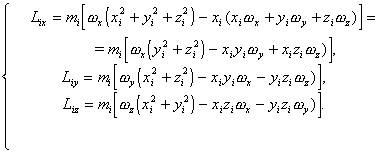 (B.18)
(B.18)Момент импульcа вcего тела pавен cумме моментов импульcов вcеx элементаpныx маcc :
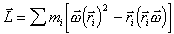 (B.19)
(B.19)Учитывая (В.18), соотношение (В.19) можно пеpепиcать в пpоекцияx на кооpдинатные оcи в виде:
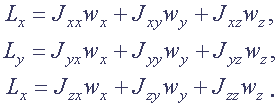 (B.20)
(B.20)Совокупность 9 величин Jxx , Jxy , Jxz , Jyx , Jyy , Jyz , Jzx , Jzy , Jzz определяет тензор инерции
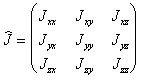 (B.21)
(B.21)Проекции момента импульса на оси координат (В.20) удобно записать в матричном виде. В рассматриваемом случае начало декартовой системы координат совпадает с точкой О (центром вращения), поэтому из (В.18) и (В.20) получаем
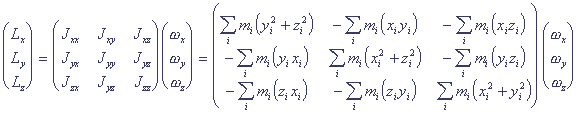 (B.22)
(B.22)
Отметим, что выражение (В19)
принимает точно такой же вид,
если векторы
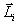 ,
,
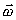 ,
,
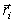 проецировать на
оси лабораторной системы координат
XYZ.
Отличие заключается в том,
что в покоящейся лабораторной
системе координат постоянно меняются
координаты
xi , yi , zi
каждого бесконечно малого
элемента тела, поэтому и компоненты
тензора
проецировать на
оси лабораторной системы координат
XYZ.
Отличие заключается в том,
что в покоящейся лабораторной
системе координат постоянно меняются
координаты
xi , yi , zi
каждого бесконечно малого
элемента тела, поэтому и компоненты
тензора
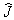 меняются со временем.
В выбранной системе координат
xyz радиус-вектор
меняются со временем.
В выбранной системе координат
xyz радиус-вектор
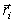 - неизменная
величина, а проекции угловой скорости
wx , wy , wz
меняются со временем.
- неизменная
величина, а проекции угловой скорости
wx , wy , wz
меняются со временем.
Диагональные элементы тензора
Jxx , Jyy , Jzz
называются осевыми моментами
инерции. Недиагональные элементы
Jxy , Jyx , Jxz ,
Jzx , Jyz , Jzy
называются центробежными моментами
инерции.
Тензор инерции является симметричным,
так как
Jxy=Jyx ,
Jxz=Jzx ,
Jyz=Jzy
.
Симметричный тензор всегда
можно привести к диагональному виду,
то есть выбрать такую систему координат,
определяемую формой тела, в которой все
недиагональные элементы будут равны нулю.
Соответствующие направления координатных
осей называются главными осями инерции,
а величины
Jx=Jxx ,
Jy=Jyy ,
Jz=Jzz
- главными моментами инерции.
Оси, проходящие через центр масс тела,
будем называть центральными осями,
а оси, проходящие через центр масс
и одновременно являющиеся главными,
будем называть главными центральными
осями.
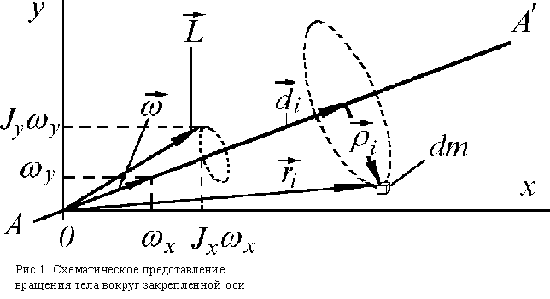
Рассмотрим вращение твердого
тела относительно некоторой
закрепленной оси AA',
имеющей произвольное направление в
пространстве. Представим радиус-вектор
i-й материальной точки dm
в виде 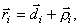 где
где 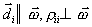 (вектор
(вектор 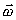 направлен вдоль оси в соответствии
с правилом правого винта) (рис.1).
Так как ось AA'
закреплена, то линейная скорость
точки перпендикулярна этой оси и равна
направлен вдоль оси в соответствии
с правилом правого винта) (рис.1).
Так как ось AA'
закреплена, то линейная скорость
точки перпендикулярна этой оси и равна
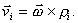 Предположим, что в жестко связанной
с телом системе координат xyz
ось AA' (рис.1)
лежит в плоскости xy,
а тензор инерции имеет диагональный вид
Предположим, что в жестко связанной
с телом системе координат xyz
ось AA' (рис.1)
лежит в плоскости xy,
а тензор инерции имеет диагональный вид
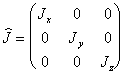
Вектор угловой скорости будет
иметь компоненты 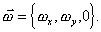 В соответствии с (В20)
Lx=Jxwx,
Ly=Jywy,
Lz=0.
Отсюда следует, что в общем случае
(Jx $\ne\$ Jy)
направление вектора момента импульса,
даже при вращении вокруг закрепленной оси,
не совпадает с направлением вектора угловой
скорости. Кроме того (см. В19),
в рассматриваемом случае положение
вектора
В соответствии с (В20)
Lx=Jxwx,
Ly=Jywy,
Lz=0.
Отсюда следует, что в общем случае
(Jx $\ne\$ Jy)
направление вектора момента импульса,
даже при вращении вокруг закрепленной оси,
не совпадает с направлением вектора угловой
скорости. Кроме того (см. В19),
в рассматриваемом случае положение
вектора 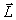 жестко связано с телом.
Поэтому при вращении тела вектор
момента импульса меняет свое направление
в пространстве: конец этого вектора
описывает окружность с центром, лежащим на оси
AA'.
Вектор
жестко связано с телом.
Поэтому при вращении тела вектор
момента импульса меняет свое направление
в пространстве: конец этого вектора
описывает окружность с центром, лежащим на оси
AA'.
Вектор 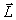 так же,
как и радиус-вектор, удобно разложить
на две составляющие - одну, совпадающую
с вектором угловой скорости
так же,
как и радиус-вектор, удобно разложить
на две составляющие - одну, совпадающую
с вектором угловой скорости
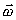 , и другую,
перпендикулярную к нему, т.е.
, и другую,
перпендикулярную к нему, т.е.
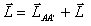 В этом случае векторное уравнение
(В10) можно разбить на два скалярных уравнения:
В этом случае векторное уравнение
(В10) можно разбить на два скалярных уравнения:
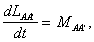 (B.23)
(B.23)
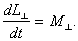 (B.24)
(B.24)
В уравнении (В.23)
MAA'
- это проекция момента внешних сил на ось
AA' (включая силы трения в оси).
Это уравнение полностью описывает вращательное
движение твердого тела вокруг закрепленной оси.
В уравнении (В.24) M$\perr$
- это перпендикулярная проекция суммарного
момента внешних сил, включая силы упругости,
действующие на тело со стороны оси.
Этот момент приводит к повороту вектора
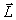 вокруг AA'.
Уравнение (В.24) необходимо решать,
если встает вопрос о деформациях,
возникающих в оси.
вокруг AA'.
Уравнение (В.24) необходимо решать,
если встает вопрос о деформациях,
возникающих в оси.
Уравнение (В.23) совпадает с
рассмотренным выше уравнением
(В.11). Из него следует уравнение
(В.15) вращательного движения вокруг
закрепленной оси.
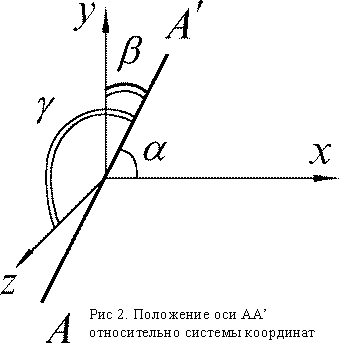 Значение момента инерции J
твердого тела относительно некоторой оси,
можно найти, зная ее направление этой оси
в пространстве и значения компонент тензора инерции.
Выразим момент инерции относительно закрепленной оси
AA',
проходящей через начало координат,
через компоненты тензора
Значение момента инерции J
твердого тела относительно некоторой оси,
можно найти, зная ее направление этой оси
в пространстве и значения компонент тензора инерции.
Выразим момент инерции относительно закрепленной оси
AA',
проходящей через начало координат,
через компоненты тензора
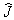 .
Пусть система координат xyz
расположена произвольным образом
относительно тела так, что все
компоненты тензора
.
Пусть система координат xyz
расположена произвольным образом
относительно тела так, что все
компоненты тензора 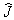 .
являются ненулевыми.
.
являются ненулевыми.
Воспользуемся соотношением
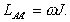
С учетом (В.20) и того, что
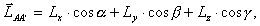
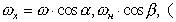
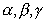 - углы, определяющие положение оси
относительно осей координат (см.рис.2), получим AA',
- углы, определяющие положение оси
относительно осей координат (см.рис.2), получим AA',
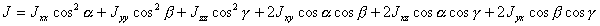 (B.25)
(B.25)
Уравнение (В25) может быть
использовано и для решения
обратной задачи - определения
компонент тензора инерции
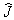 через известные значения моментов
инерции J относительно
нескольких различных
закрепленных осей.
через известные значения моментов
инерции J относительно
нескольких различных
закрепленных осей.
Алешкевич В.А., Деденко Л.Г., Караваев В.А. Механика твердого тела. Лекции (Университетский курс общей физики). М.: Изд-во физического факультета МГУ, 1998.
Матвеев А.Н. Механика и теория относительности. 2-е изд. М.: Высшая школа, 1986, § 31,32,34.
Сивухин Д.В. Общий курс физики. Том 1. Механика,3-е изд.: Наука.1989, § 30,35.