Используется пружинный маятник, тело которого движется в
вязкой среде, а внешняя вынуждающая
сила создаетсяя с помощью переменного
магнитного поля. Для анализа движения
маятника используется
пьезоэлектрический датчик
силы натяжения пружины,
управление
экспериментом
и обработка результатов
производится с помощью ЭВМ.
Уравнение колебаний. Колебания широко распространены в природе. В общем случае под колебаниями понимают движения, в том или иной степени повторяющиеся во времени. По физической природе изменяющейся величины колебательные процессы разделяют на механические, электромагнитные, электромеханические и т.д. Особую роль в физике играют механические и электромагнитные колебания. С помощью распространяющихся колебаний плотности и давления воздуха (воспринимаемых как звук) и с помощью распространяющихся электромагнитных колебаний (свет) мы получаем большую часть информации об окружающем мире.
Несмотря на различную физическую природу колебаний, все они обладают некоторой общей сущностью, которая в первую очередь определяется возможностью их единообразного математического описания.
Все колебания могут быть разбиты на три группы: периодические, квазипериодические и непериодические. Периодическими колебаниями мы называем те процессы, которые повторяются во времени и описываются такой функцией времени, что f(t)=f(t+T), где Т — период данного колебания. Квазипериодическими колебаниями называются такие непериодические колебания, которые в течение длительного времени сохраняют основные характеристики процесса при медленном изменении их параметров (например, амплитуды).
Если уравнения, описывающие колебания, имеют вид линейных дифференциальных уравнений, колебания называются линейными. Физически это соответствуют тем случаям, когда в системе все возникающие силы можно считать линейными функциями координат и скоростей.
Колебательный процесс в системе может возникнуть в двух случаях. В первом из них за счет внешней силы система выводится из состояния устойчивого равновесия, т.е. ей сообщается некоторое достаточное количество потенциальной или кинетическоэй энергии, после чего внешние силы полностью отключаются. Тогда, за счет работы внутренних сил, образующихся в ситеме, происходит переход кинетической энергии в потенциальную и наоборот. В этом случае возникают колебания, которые называются свободными или собственными колебаниями системы. Если же на систему постоянно действует внешняя сила, то возникают так называемые вынужденные колебания.
Если физическая величина x(t) изменяется со временем по гармоническому закону
 (1)
(1) — круговая частота (T — период);
t — время;
— круговая частота (T — период);
t — время;
 0 —начальная
фаза колебаний. Функция х{t)
из (1) представляет решение
дифференциального уравнения
0 —начальная
фаза колебаний. Функция х{t)
из (1) представляет решение
дифференциального уравнения
 (2)
(2)Физическую систему, выведенную из состояния равновесия и представленную самой себе, в которой изменение одного из параметров х описывается дифференциалльным уравнением (2) называют классическим гармоническим осциллятором.
Действие классического гармонического осциллятора на примере пружинного маятника показана ниже. В апплете можно изменять следующие параметры А - амплитуда колебаний или начальное отклонение, m - масса маятника и k - коэффициент жесткости пружины. Стоит так же отметить, что в нашей модели, следующие начальные условия: t=0 , v(0)=0 , x(0)=A, как и в лабораторной работе. Кроме функции x(t), можно наблюдать v(t), a(t) .
Обсудим реализацию гармонического осциллятора на примере пружинного маятника.
Собственные колебания пружинного маятника. Пружинный маятник состоит из тела массы m и легкой пружины с коэффициентом жесткости k (рис.1, а). В общем случае движение пружинного маятника в поле силы тяжести довольно сложно и описывается большим числом степеней свободы. Практический интерес, однако, представляют колебания с одной степенью свободы, когда движение маятника происходит вдоль вертикальной оси. Для того, чтобы маятник совершал только вертикальные колебания достаточно оттянуть тело строго вниз на небольшую величину (рис.1, б,в ). Для полного описания колебаний в этом случае необходимо знать поведение только одной переменной, например, вертикальной координаты центра масс тела маятника. На тело, подвешенное на пружине в поле силы тяжести действуют две силы (без учета сил трения) сила тяготения и упругая сила. Начало координат выберем таким образом, чтобы при х=О масса m находилась в равновесии. При этом сила тяжести mg будет скомпенсирована некоторым начальным растяжением пружины и в дальнейшем рассмотрении участвовать не будет.
При отклонении тела от точки равновесия будет возникать возвращающая сила F(х). Рассмотрим малые колония пружинного маятника. Колебания пружиннного маятника называют малыми, если сила, возникающая при смещении грузика от положения равновесия, пропорциональна его смешению и направлена в сторону положения равновесия. Для пружиннного маятника условия малости колебаний удовлетворяются при смещениях, создающих возвращающую силу у пружины в пределах применимости закона Гука. Уравнение движения пружинного маятника при этом имеет вид
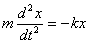 (3)
(3)Сравнивая с (2), имеем
 (4)
(4)В реальных осцилляторах, за счет сил трения, происходит рассеяние (диссипация) запасенной энергии, в результате чего свободные колебания со временем затухают. При движения тела пружинного маятника в вязкой среде, с небольшими скоростями сила трения пропорциональна скорости
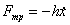 .
При учет диссипации энергии уравнение
колебаний пружинного маятника имеет
вид линейного дифференциального
уравнения второй степени
.
При учет диссипации энергии уравнение
колебаний пружинного маятника имеет
вид линейного дифференциального
уравнения второй степени
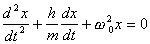 (5)
(5)Решение этого уравнения имеет вид затухающих колебаний
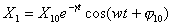 (6)
(6)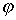 10
— начальные амплитуда и фаза
колебаний, w — частота
затухающих колебаний,
10
— начальные амплитуда и фаза
колебаний, w — частота
затухающих колебаний,
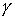 — декремент затухания.
Действительно, подставим
(6) в (5) получим
— декремент затухания.
Действительно, подставим
(6) в (5) получим
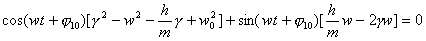 (7)
(7)Отсюда следует, что
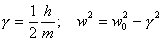 (8)
(8)Используя полученный результат уравнение колебаний удобно записать в виде:
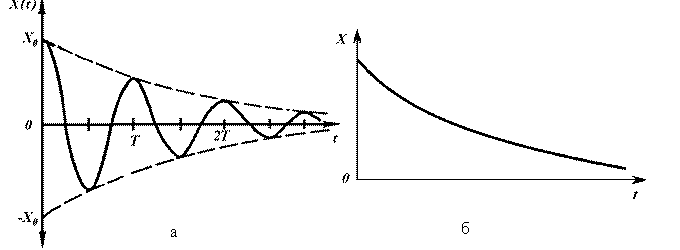
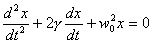 (9)
(9)Отклонения маятника от положения равновесия в зависимости от времени в соответствии с (6) имеет вид показанный на рис. 2,a. Для малых декрементов затухания колебания близки к гармоническим, при больших
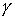 затухание происходит за 1—2
периода. В том случае, когда
затухание происходит за 1—2
периода. В том случае, когда
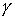
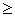 w0
значение частоты w
становится мнимым и гармонические
колебания не реализуются, происходит
апериодический процесс—тело
маятника после начального
отклонения плавно возвращается
в положение
равновесия (см. рис.2, б),
w0
значение частоты w
становится мнимым и гармонические
колебания не реализуются, происходит
апериодический процесс—тело
маятника после начального
отклонения плавно возвращается
в положение
равновесия (см. рис.2, б),
Величина
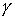 получила название декремента затухания.
При этом величина
получила название декремента затухания.
При этом величина 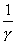 равна времени, за которое
амплитуда колебаний затухает в е
раз. Затухание колебаний за период
равна времени, за которое
амплитуда колебаний затухает в е
раз. Затухание колебаний за период
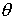 =
= 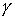 Т
носит название логарифмического
декремента затухания, его можно
определить из соотношения
Т
носит название логарифмического
декремента затухания, его можно
определить из соотношения
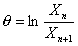 (10)
(10)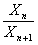 — отношение амплитуд двух последовательных
колебаний.
— отношение амплитуд двух последовательных
колебаний.
Вынужденные колебания пружинного маятника. Рассмотрим теперь колебания пружинного маятника, которые возникают под действием внешней периодической силы
Fвн(t)
 0
в системе с одной степенью
свободы. Вынужденные колебания
в случае гармонического
воздействия
описываются уравнением
0
в системе с одной степенью
свободы. Вынужденные колебания
в случае гармонического
воздействия
описываются уравнением
 (11)
(11)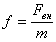 — нормированная амплитуда
вынуждающей силы, w —
частота вынуждающей силы.
Решение уравнения (11) имеет вид
— нормированная амплитуда
вынуждающей силы, w —
частота вынуждающей силы.
Решение уравнения (11) имеет вид
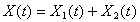 (12)
(12)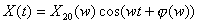 (13)
(13)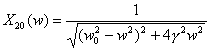 (14)
(14)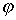 (w)
— зависящая от частоты фаза колебаний, причем
(w)
— зависящая от частоты фаза колебаний, причем
 (15)
(15)Выражения для амплитуды и фазы колебаний, также как и для свободных колебаний, можно определить, непосредственной подстановкой (13) в (11). При малых декрементах затухания на частотах вблизи частоты w
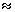 w0
свободных колебаний маятника амплитуда колебаний
резко воозрастает.
Это явление получило
название резонанса.
Более точно
значение резонансной
частоты wрез
можно получить из (14),
проводя исследование функции на экстремум
w0
свободных колебаний маятника амплитуда колебаний
резко воозрастает.
Это явление получило
название резонанса.
Более точно
значение резонансной
частоты wрез
можно получить из (14),
проводя исследование функции на экстремум
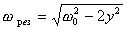 (16)
(16)В этом апплете представлены вынужденные колебания пружинного маятника. Этот случай, как было сказано выше, описывается уравнением (11). Важная особенность этого случая заключается в том, что менять частоту вынуждающей силы, то можно добиться резонанса. Так же вы можете наблюдать установление вынужденных колебаний.
Типичные амплитудно—частотные и фазочастотные характеристики показании на рис.3
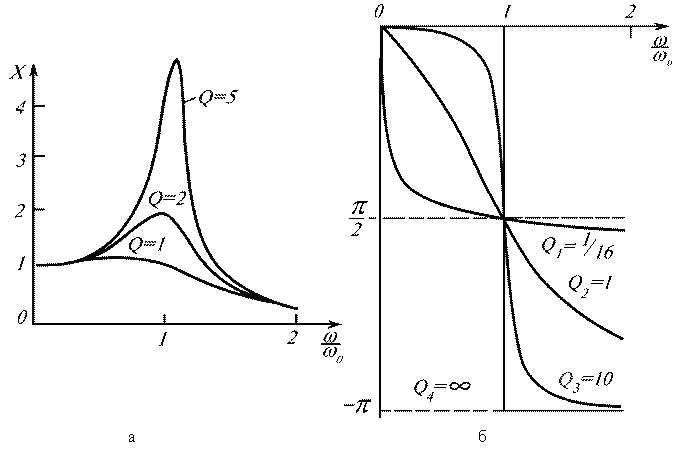
Семейство амплитудно-частотных характеристик u - относительная амплитуда смещения
c - относительная амплитуда скорости
w - относительная амплитуда ускорения
Q - декремент затухания
кнопка "старт" запускает апплет, кнопка "+" позволяет к нарисованным графикам добавлять другие. Кнопка "сброс" позволяет нарисовать новое семейство графиков при других параметрах.
 При анализе резонансных
кривых в системах с различным
затуханием наряду с
декрементом затухания
При анализе резонансных
кривых в системах с различным
затуханием наряду с
декрементом затухания  ,
логарифмическим декрементом затухания
,
логарифмическим декрементом затухания
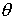 широко пользуются
величиной , которая называется
добротностью системы Q.
Она определяется как отношение амплитуды
смещения при резонансе ( w = w0 ) X2рез
к амплитуде смещения Xcт
при
широко пользуются
величиной , которая называется
добротностью системы Q.
Она определяется как отношение амплитуды
смещения при резонансе ( w = w0 ) X2рез
к амплитуде смещения Xcт
при  0.
Учитывая определения коэффициента
затухания, логарифмического
декремента затухания,
а также соотношение
(14), получаем
0.
Учитывая определения коэффициента
затухания, логарифмического
декремента затухания,
а также соотношение
(14), получаем
 (17)
(17)Можно показать, что в случае, когда Q > 1 добротность можно выразить также через ширину резонансной кривой (см.рис.4)
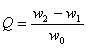 (18)
(18)
Исследование колебаний маятника
проводится на установке, схема
которой приведена на рис.5.
Установка состоит из пружинного
маятника, системы регистрации
колебаний на основе пьезоэлектрического
датчика, системы возбуждения вынужденных
колебаний, а также системы
обработки информации на
персональном компьютере.
Исследуемый пружинный маятник
состоит из стальной пружины с
коэффициентом жесткости k
и тела маятника m,
в центре которого вмонтирован
постоянный магнит. Движение
маятника происходит в жидкости
и при
небольших скоростях
колебаний возникающая сила
трения может быть с
достаточной точностью аппроксимирована
линейным законом, т.е.
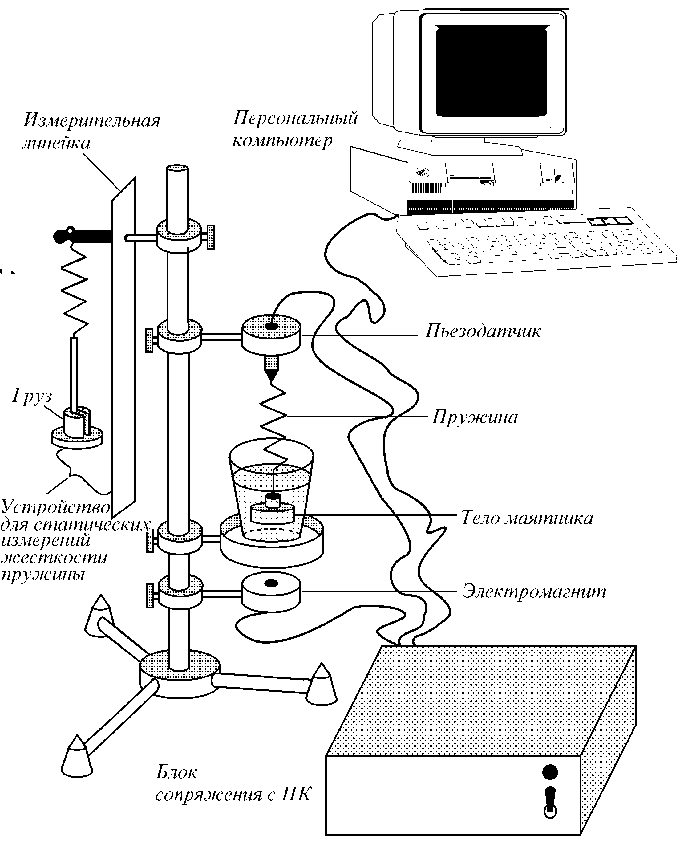

Для увеличения силы сопротивления при движении в жидкости, тело маятника изготовлено в виде шайбы с отверстиями. Для регистрации колебаний используется пьезоэлектрический датчик, к которому подвешена пружина маятника. Во время движения маятника сила упругости пропорциональна смещению х,
Так как ЭДС, возникающая в пьезодатчике в свою очередь пропорциональна силе давления, то сигнал, получаемый с датчика будет пропорционален смещению тела маятника от положения равновесия.
Возбуждение колебаний осуществляется с помощью магнитного поля. Гармонический сигнал, создаваемый ПК усиливается и подается на катушку возбуждения, расположенную под телом маятника. В резултате этого катушки образуется переменное во времени и неоднородное в пространстве магнитное поле. Это поле действует на постоянный магнит, вмонтированный в тело маятника и создает внешнюю периодическую силу. При движении тела вынуждающую силу можно представить в виде суперпозиции гармонических функций
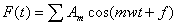 , и колебания маятника будут являться
суперпозицией колебаний с частотами mw.
Однако заметное влияние на движение маятника
будет оказывать лишь составляющая силы на
частоте w ,
так как она наиболее близка к резонансной частоте.
Поэтому амплитуды
составляющих колебаний
маятника на частотах mw
будут малы.
То есть в случае
произвольного
периодического воздействия
колебания с большой степенью
точности можно считать гармоническими на
частоте w.
, и колебания маятника будут являться
суперпозицией колебаний с частотами mw.
Однако заметное влияние на движение маятника
будет оказывать лишь составляющая силы на
частоте w ,
так как она наиболее близка к резонансной частоте.
Поэтому амплитуды
составляющих колебаний
маятника на частотах mw
будут малы.
То есть в случае
произвольного
периодического воздействия
колебания с большой степенью
точности можно считать гармоническими на
частоте w.
Система обработки информации состоит из аналого-цифрового преобразователя и персонального компьютера. Аналоговый сигнал с пьезоэлектрического датчика с помощью аналоге—цифрового преобразователя представляется в цифровом виде и подается на персональном компьютере.
После включения компьютера и загрузки программы на экране мо- нитора появляется основное меню, общий вид которого показан на рис.5. Используя клавиши управления курсором
 ,
,  ,
,  ,
,  ,
можно выбрать
один из пунктов меню.
После нажатия кнопки ENTER
компьютер приступает к
выполнению выбранного режима
работы. Простейшие подсказки
по выбранному режиму работы
содержатся в выделенной строке
внизу экрана.
,
можно выбрать
один из пунктов меню.
После нажатия кнопки ENTER
компьютер приступает к
выполнению выбранного режима
работы. Простейшие подсказки
по выбранному режиму работы
содержатся в выделенной строке
внизу экрана.
Рассмотрим возможные режимы работы программы:
Статика — этот пункт меню используется для обработки результатов первого упражнения (см. рис.5) После нажатия на кнопку ENTER компьютер запрашивает массу груза маятника. После следующего нажатия кнопки ENTER на экране появляется новая картинка с мигающим курсором. Последовательно записывают на экране массу груза в граммах и, после нажатия пробела, величину растяжения пружины. Нажав на ENTER переходят на новую строку и снова записывают массу груза и величину растяжения пружины. Допускается редактирование данных в пределах последней строки. Для этого нажав клавишу Backspase удаляют неправильное значение массы или растяжения пружины и записывают новое значение. Для изменения данных в других строках необходимо последовательно нажать Esc и ENTER, а затем повторить набор результатов.
После набора данных нажимают на функциональную клавишу F2. На экране появляются расчитанные с помощью метода наименьших квадратов значения коэффициента жесткости пружины и частоты свободных колебаний маятника. После нажатия на ENTER на экране монитора появляется график зависимости упругой силы от величины расрастяжения пружины. Возврат в основное меню происходит после нажатия любой клавиши.
Эксперимент — этот пункт имеет несколько подпунктов (рис.6). Рассмотрим особенности работы каждого из них.
Частота — в этом режиме с помощью клавиш управления курсором осуществляется задание частоты вынуждающей силы. В том случае, если проводится эксперимент со свободными колебаниями, то необходимо установить значение частоты равное 0.
Старт — в этом режиме после нажатия кнопки ENTER программа начинает снимать экспериментальную зависимость отклонения маятника от времени. В том случае, когда частота вынуждающей силы равна нулю, на экране появляется картина затухающих колебаний. В отдельном окошке записываются значения частоты колебаний и постоянной затухания. Если частота возбуждающей силы не равна нулю, то наряду с графиками зависимостей отклонения маятника и вынуждающей силы от времени на экране в отдельных окошках записываются значения частоты вынуждающей силы и ее амплитуды, а также измеренных частоты и амплитуды колебаний маятника. Нажав на клавишу Esc можно выйти в основное меню.
Сохранить — если результат эксперимента удовлетворителен, то его можно сохранить, нажав на соответствующую клавишу меню.
Нов. Серия — этот пункт меню используется в том случае, если возникла необходимость отказаться от данных текущего эксперимента. После нажатия клавиши ENTER в этом режиме из памяти машины стираются результаты всех предыдущих экспериментов, и можно начать новую серию измерений.
После проведения эксперимента переходят в режим Измерения. Этот пункт меню имеет несколько подпунктов (рис.7)
График АЧХ — этот пункт меню используется после окончания эксперимента по изучению вынужденных колебаний. На экране монитора строится амллитудно-частотная характеристика вынужденных колебаний.
График ФЧХ — В этом режиме после окончания эксперимента по изучению вынужденных колебаний на экране монитора строится фазочастотная характеристика.
Таблица — этот пункт меню позволяет выдать на экран монитора значения амплитуды и фазы колебаний в зависимости от частоты вынуждающей силы. Эти данные переписываются в тетрадь для отчета по данной работе.
Пункт меню компьютера Выход — окончание работы программы (см. например, рис. 7)
Упражнение 1. Определение коэффициента жесткости пружины статическим методом.
Измерения проводятся путем определения удлинения пружины под действием грузов с известными массами. Рекомендуется провести не менее 7—10 измерений удлинения пружины постепенно подвешивая грузы и изменяя тем самым нагрузку от 20 до 150 г. Используя пункт меню работы программы Статистика результаты этих измерений заносят в память компьютера и определяют коэффициент жесткости пружины используя метод наименьших квадратов. В ходе выполнения упражнения необходимо расчитать значение собственной частоты колебаний маятника
 (19)
(19)Отчет по упражнению N 1 должен содержать таблицу зависимости удлинения пружины х от массы подвешиваемых грузов М, график этой зависимости (см. рис. 8), расчитанные значения k, w и их погрешности.
Упражнение 2. Определение частоты свободных колебаний пру- жинного маятника и декремента затухания.
Для выполнения этого упражнения выбранный маятник подвешивают на установку. Устанавливают зазор между маятником и дном стакана около 1 см. Во время выполнения упражнения в пункте меню Частота (см. рис. 9) устанавливается значение частоты, равное нулю. После этого нажимают кнопку "старт" в меню программы. После этого на маятник с персонального компьютера падается возбуждающее воздействие. Через некоторое время на экране монитора строится зависимость скорости затухающих колебаний от времени и выводятся результаты расчета частоты и коэффициента затухания (рис. 10). Измерения проводят 5—7 раз. Условно считая эти измерения прямыми, находят значения частоты и декремента затухания для собственных колебаний пружинного маятника. Проводят сравнение частоты собственных колебаний со значением, найденным из первого упражнения по формуле (19). Отчет по этому упражнению должен содержать таблицу результатов измерений значений частоты и декремента затухания для собственных колебаний и их стандартные отклонения.
Упражнение 3. Изучение вынужденных колебаний пружинного маятника.
Целью этого упражнения является снятие амплитудно-частотной (АЧХ) и фазо—частотной (ФЧХ) характеристики вынужденных колебаний. При снятии частотных характеристик пользуясь пунктом меню частота выбирают значение частоты v. Частоту выбирают таким образом , чтобы
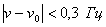 , где v0
— частота собственных колебаний,
найденная из второго упражнения.
Амплитуда вынужденных колебаний
маятника в этом диапазоне частот
должна быть не менее 2—5 мм.
При снятии АЧХ и ФЧХ следует помнить, что в системе могут одновременно
возбуждаться собственные и вынужденные колебания, поэтому при
изменении частоты генератора каждый раз нужно выжидать некоторое
время
, где v0
— частота собственных колебаний,
найденная из второго упражнения.
Амплитуда вынужденных колебаний
маятника в этом диапазоне частот
должна быть не менее 2—5 мм.
При снятии АЧХ и ФЧХ следует помнить, что в системе могут одновременно
возбуждаться собственные и вынужденные колебания, поэтому при
изменении частоты генератора каждый раз нужно выжидать некоторое
время  t, чтобы собственные колебания маятника успевали затухнуть.
Значение времени
t, чтобы собственные колебания маятника успевали затухнуть.
Значение времени  t
следует определить по формуле
t
следует определить по формуле
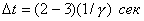 (20)
(20)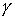 — коэффициент затухания, найденный из второго упражнения.
— коэффициент затухания, найденный из второго упражнения.
Для определения амплитуды и фазы вынужденных колебаний при заданной частоте следует выбрать пункт меню Старт и нажать кнопку ENTER. На экране монитора при этом выводятся зависимости вынуждающей силы и скорости маятника от времени, а также результаты расчета амплитуды и частоты вынуждающей силы, амплитуды, частоты и фазы колебаний маятника ( рис. 11). В том случае, если относительная разность между значениями частоты вынуждающей силы и частоты генератора не превышает величины одного процента, можно считать, что собственные колебания затухли. Эти результаты следует запомнить, нажав ENTER в режиме Сохранить.
Снимать амплитудно— и фазо—частотные характеристики следует тщательно, особенно в области резкого изменения амплитуды и фазы. Для этого следует менять частоту возбуждающей силы каждый раз не более чем на 0,05 Гц. Расчитанные на компьютере значения амплитуды и фазы колебаний следует занести в таблицу, а затем по этим данным построить графики. Используя пункты меню график АЧХ и График ФЧХ, можно просмотреть на экране монитора АЧХ и ФЧХ ( рис. 12 и 13).
Используя фазо-частотную характеристику, следует определить ко- эффициент затухания по формуле (вывод формулы см. в приложении)
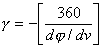
а также значение добротности по формуле где vрез — резонансная частота.
Полученное значение декремента затухания следует сравнить с
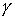 ,
найденным во втором
упражнении. Значение
добротности можно также
оценить по АЧХ. Измерив
ширину резонансной кривой
,
найденным во втором
упражнении. Значение
добротности можно также
оценить по АЧХ. Измерив
ширину резонансной кривой
 v
на уровне значения амплитуды, равного
v
на уровне значения амплитуды, равного
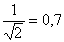 от значения амплитуды при резонансе
(v = vрез ),
получают оценку добротности Q
(справедливую при малом затухании,
когда
от значения амплитуды при резонансе
(v = vрез ),
получают оценку добротности Q
(справедливую при малом затухании,
когда  v « v)
v « v)

Отчет по третьему упражнению должен содержать таблицу зависимостей амплитуды и фазы колебаний от частоты, АЧХ и ФЧХ, а также результаты расчета
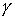 и Q.
и Q.
В результате работы должно быть определена собственная частота колебаний пружинного маятника, декремент затухания и получены его амплитудно-частотные и фазо-частотные характеристики.
Приложение
Расчет коэффициента затухания по ФЧХ
Известно, что сдвиг фазы
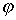 вынужденных колебаний зависит от
частоты w
и коэффициента затухания
вынужденных колебаний зависит от
частоты w
и коэффициента затухания
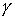 следующим образом
следующим образом
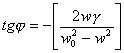 (п.1)
(п.1)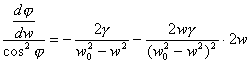 (п.2)
(п.2)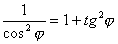 ,
то используя (п.1) имеем
,
то используя (п.1) имеем
 (п.3)
(п.3) (п.4)
(п.4)При выполнении работы сдвиг фаз
 измеряется не в радианах, а в
градусах, а фазовая зависимость
строится не от w,
а от частоты колебаний
измеряется не в радианах, а в
градусах, а фазовая зависимость
строится не от w,
а от частоты колебаний
 , поэтому можно записать
, поэтому можно записать
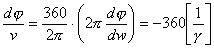 (п.5)
(п.5)В качестве приложения так же приведем апплет фазовых траекторий для вынужденных колебаний.